Wenn die Besucherzahlen deiner Website nicht so hoch sind wie erhofft, ist das kein Grund, deine Ziele bei der Conversion-Rate-Optimierung (CRO) aufzugeben.
Mittlerweile hast du sicher bemerkt, dass die meisten Tipps zur CRO auf Websites mit einem hohen Traffic zugeschnitten sind. Zum Glück bedeutet das aber nicht, dass du deine Website nicht auch dann optimieren kannst, wenn du weniger Besucher hast.
De facto kann jede Website optimiert werden – Du musst nur deine Optimierungsstrategie an deine einzigartige Situation anpassen.
In diesem Artikel greifen wir folgende Punkte auf:
- Die häufigste Klage über CRO (95 %-Schwelle und Ursprung)
- Ein angemessener Schwellenwert für geringen Traffic
- Ideen, wie du deine Website bei einem geringeren Traffic optimieren kannst
- Die CUPED-Testtechnik
- Wann CUPED funktioniert und wann nicht
CRO-Analogie
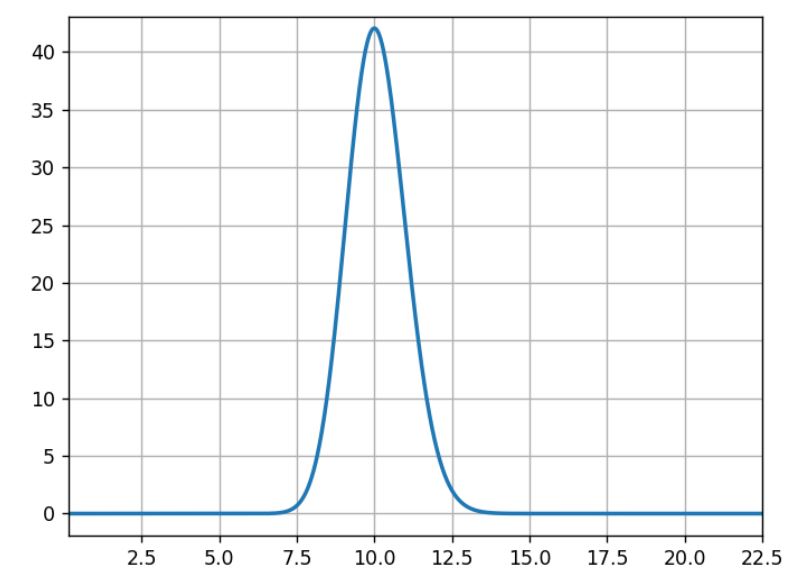
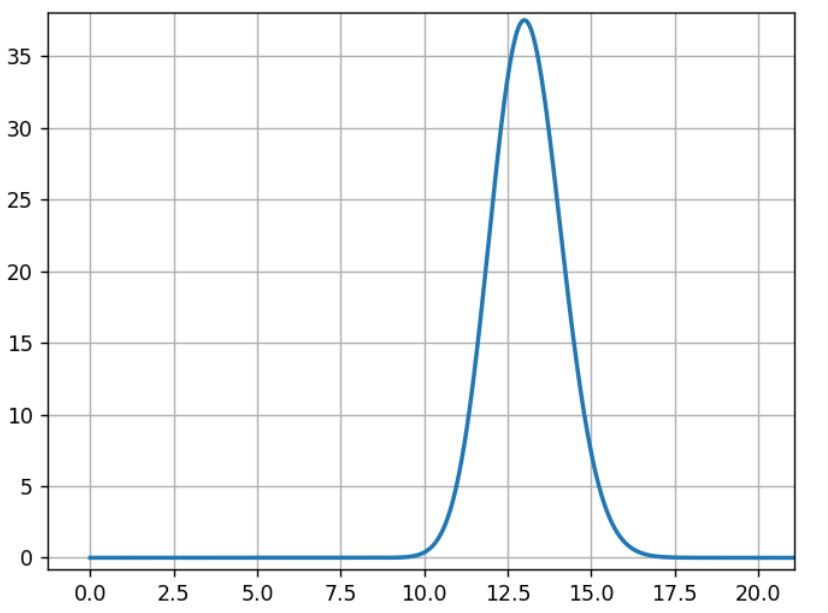
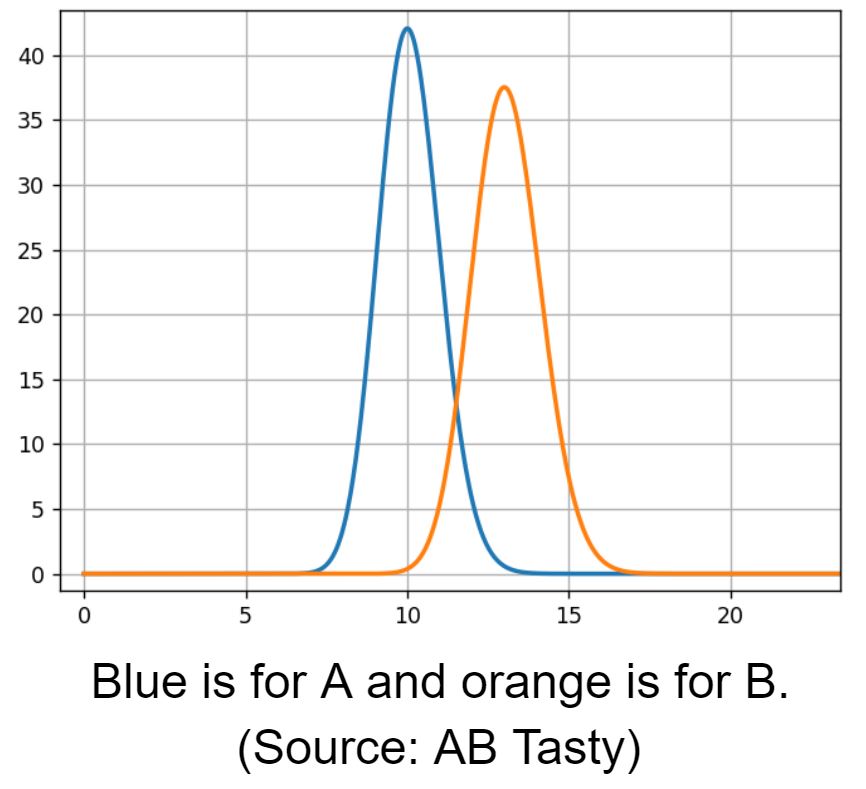
Um diesen Artikel besser verstehen zu können, beginnen wir mit einer Analogie. Stell dir vor, statt zwei Varianten zu messen und einen Gewinner zu ermitteln, messen wir die Leistung von zwei Boxern und schließen Wetten ab, wer die nächsten 10 Runden gewinnt.
Wie können wir also auf den Sieger setzen?
Stell dir vor, dass Boxer A und Boxer B beide Newcomer sind, die keiner kennt. Nach der ersten Runde musst du deine Wahl treffen. Im Endeffekt wirst du mit großer Wahrscheinlichkeit auf den Boxer setzen, der die erste Runde gewonnen hat. Die Entscheidung mag riskant sein, wenn der Vorsprung des Siegers gering ist. Du kannst deine Entscheidung letztlich jedoch nicht auf einer anderen Grundlage treffen.
Stell dir nun vor, dass Boxer A als Champion bekannt ist und Boxer B ein Herausforderer ist, den du nicht kennst. Dein Wissen über Boxer A bezeichnen wir als Prior – Informationen, die du bereits hast und die deine Entscheidung beeinflussen.
Aufgrund dieses Priors oder Vorwissens ist es wahrscheinlicher, dass du in den nächsten Runden auf Boxer A setzt, selbst wenn Boxer B die erste Runde mit einem äußerst kleinen Vorsprung gewinnt.
Zudem wirst du den Boxer B nur dann als voraussichtlichen Sieger wählen, wenn er die erste Runde mit einem großen Vorsprung gewinnt. Je größer der Prior ist, desto größer muss der Vorsprung sein, um dich zu überzeugen, deine Wettentscheidung zu ändern.
Kannst du mir folgen? Wenn ja, sind die folgenden Abschnitte leicht zu begreifen und du wirst verstehen, woher diese „95 %-Schwelle“ kommt.
Kommen wir nun zu den Tipps für die Optimierung deiner Website mit geringem Traffic.
1. Die Lösung des Problems: „Ich erreiche nie die 95 %ige Signifikanz“.
Das ist die häufigste Klage, die man über CRO für Websites mit geringem Traffic und für Seiten mit geringem Traffic auf größeren Websites hört.
Bevor wir uns diesem häufigsten Problem widmen, sollten wir zunächst die Frage beantworten, woher diese „goldene Regel“ der 95 % stammt.
Ursprung der 95 %-Schwelle
Beginnen wir unsere Erklärung mit einer sehr einfachen Idee: Was wäre, wenn Optimierungsstrategien vom ersten Tag an angewandt würden? Wenn zwei Varianten ohne Vorgeschichte gleichzeitig erstellt würden, gäbe es keine „Original“-Version, die von einem Newcomer herausgefordert werden könnte.
Dadurch wärst du gezwungen, von Anfang an die beste Version zu wählen.
In diesem Fall könnte jeder kleine Leistungsunterschied für die Entscheidungsfindung gemessen werden. Nach einem kurzen Test wirst du dich für die Variante mit der höheren Leistung entscheiden. Es wäre keine gute Strategie, die Variante mit der geringeren Leistung zu wählen, und zudem wäre es unklug, auf einen Schwellenwert von 95 % zu warten, um einen Gewinner zu ermitteln.
In der Praxis erfolgt die Optimierung jedoch erst lange nach dem Start eines Unternehmens.
In den meisten Situationen im echten Leben gibt es also eine Version A, die bereits existiert, und einen neuen Herausforderer, die Version B, die erstellt wird.
Wenn der neue Herausforderer, Version B, „auf die Bühne tritt“ und der Leistungsunterschied zwischen den beiden Varianten nicht signifikant ist, ist es für dich kein Problem, Version B nicht zum Gewinner zu erklären.
Statistische Tests sind symmetrisch. Wenn wir also die Rollen vertauschen und A und B im statistischen Test vertauschen, wirst du feststellen, dass das Original nicht deutlich besser als der Herausforderer ist. Die „Unschlüssigkeit“ des Tests ist symmetrisch.
Warum setzt du also am Ende eines nicht eindeutigen Tests 100 % des Traffics auf das Original und erklärst damit implizit A zum Sieger? Weil du drei Vorannahmen hast:
- Version A war die erste Wahl. Diese Wahl wurde vom ursprünglichen Ersteller der Seite getroffen.
- Version A wurde bereits implementiert und ist technisch vertrauenswürdig. Version B ist in der Regel ein Mockup.
- Version A verfügt über viele Daten, die ihren Wert beweisen, während Version B ein Herausforderer mit begrenzten Daten ist, die nur während der Testphase erhoben werden.
Die Punkte 1 und 2 bilden die Grundlage einer CRO-Strategie, so dass du über diese beiden Vorannahmen hinausgehen musst. Punkt 3 erläutert, dass Version A über mehr Daten verfügt, die ihre Leistung belegen, was erklärt, warum du der Version A mehr vertraust als der Version B: Version A hat Daten.
Jetzt verstehst du, dass diese 95 %-Vertrauensregel eine Möglichkeit ist, ein großes Vorwissen zu erklären. Und dieser Prior stammt meist aus historischen Daten.
Wenn du also eine Seite mit geringem Traffic optimierst, sollte der Schwellenwert deiner Entscheidung unter 95 % liegen, weil dein Prior bei A aufgrund des Traffics und des höheren Alters schwächer ist.
Der Schwellenwert sollte entsprechend dem Traffic festgelegt werden, der vom ersten Tag beim Original vorlag. Das Problem bei dieser Methode ist jedoch, dass wir wissen, dass die Conversion Rates nicht stabil sind und sich im Laufe der Zeit ändern können. Denke an die Saisonabhängigkeit – z. B. der Ansturm am Black Friday, Urlaubstage, die erhöhte Aktivität in der Weihnachtszeit, usw. Wegen der saisonalen Schwankungen kannst du die Leistungen in verschiedenen Zeiträumen nicht vergleichen.
Aus diesem Grund berücksichtigen Praktiker nur Daten für Version A und Version B, die im gleichen Zeitraum erhoben wurden, und legen einen hohen Schwellenwert (95 %) fest, um den Herausforderer als Gewinner zu akzeptieren, um einen hohen Prior gegenüber Version A zu formalisieren.
Was ist ein angemessener Schwellenwert für geringen Traffic?
Es ist schwierig, eine genaue Zahl im Auge zu haben, da diese von deiner Risikobereitschaft abhängt.
Gemäß dem Hypothesenprotokoll solltest du im Voraus einen Zeitrahmen für die Datenerhebung festlegen.
Das bedeutet, dass die „Stopp“-Kriterien eines Tests kein statistisches Maß sind oder auf einer bestimmten Zahl basieren. Die „Stopp“-Kriterien sollten einem endenden Zeitrahmen entsprechen. Sobald der Zeitraum beendet ist, solltest du die Statistiken betrachten, um eine angemessene Entscheidung zu treffen.
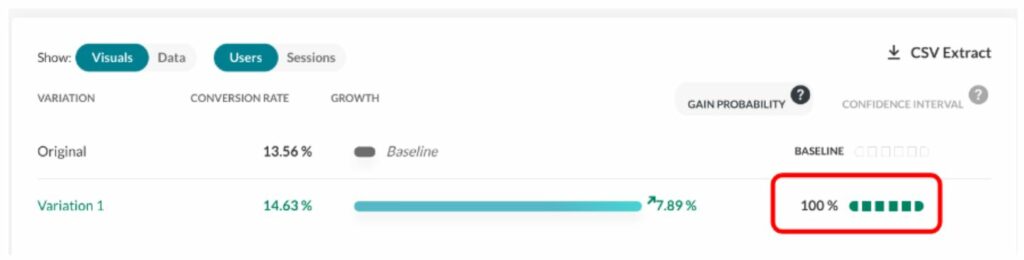
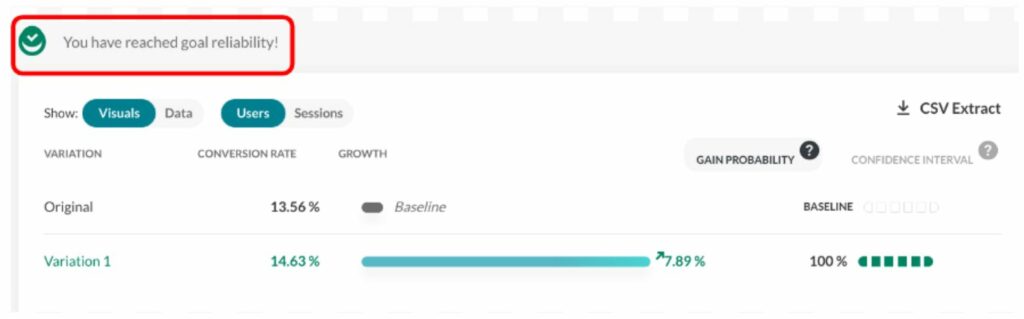
AB Tasty, unsere Software zur Optimierung der Customer Experience und zum Feature Management, verwendet das Bayessche Framework, das einen Index der „Gewinnchancen“ erzeugt, welcher eine direkte Interpretation ermöglicht – anstelle eines p-Werts mit einer sehr komplexen Bedeutung.
Mit anderen Worten, der „Index der Gewinnchancen“ ist die Wahrscheinlichkeit, dass eine bestimmte Variante besser als das Original ist.
Eine 95 %ige „Gewinnchance“ bedeutet also, dass die gegebene Variante mit 95 %iger Wahrscheinlichkeit der Gewinner sein wird. Dabei wird davon ausgegangen, dass wir kein Vorwissen oder besonderes Vertrauen in das Original haben.
Der Schwellenwert von 95 % ist auch ein Standardkompromiss zwischen dem Prior beim Original und einer bestimmten Risikoakzeptanz (es hätte auch ein Schwellenwert von 98 % sein können).
Obwohl es schwierig ist, eine genaue Zahl zu nennen, können wir eine grobe Größenordnung für den Schwellenwert angeben:
- Neue A- und B-Varianten: In einem Fall, in dem sowohl Variante A als auch Variante B neu sind, könnte der Schwellenwert bei nur 50 % liegen. Wenn es keine Daten über die Leistung der Varianten in der Vergangenheit gibt und du eine Entscheidung über die Implementierung treffen musst, ist selbst eine 51 %ige Chance auf Erfolg besser als eine 49 %ige.
- Neue Website, geringer Traffic: Wenn deine Website neu ist und einen besonders geringen Traffic aufweist, hast du wahrscheinlich einen besonders geringen Prior bei Variante A (in diesem Fall die ursprüngliche Variante). In diesem Fall ist ein Schwellenwert von 85 % angemessen. Denn wenn du das Wenige beiseite lässt, was du über das Original weißt, hast du immer noch eine 85 %ige Chance für die Auswahl des Gewinners und nur eine 15 %ige für die Auswahl einer Variante, die dem Original gleichwertig ist. Das Risiko, dass sie schlechter abschneidet, ist geringer. Je nach Kontext kann eine solche Wette also durchaus Sinn ergeben.
- Ausgereiftes Unternehmen, geringer Traffic: Wenn dein Unternehmen schon länger besteht, aber immer noch wenig Besucher zählt, sind 90 % ein vernünftiger Schwellenwert, da der Prior über das Original noch relativ klein ist.
- Ausgereiftes Unternehmen, hoher Traffic: Bei einem hohen Prior oder einer großen Menge an Daten bei Variante A wird ein Schwellenwert von 95 % empfohlen.
Der ursprüngliche Schwellenwert von 95 % ist viel zu hoch, wenn dein Unternehmen einen geringen Traffic aufweist, da die Wahrscheinlichkeit gering ist, diesen Wert zu erreichen. Demzufolge wird deine CRO-Strategie wirkungslos sein und eine datengestützte Entscheidungsfindung wird unmöglich.
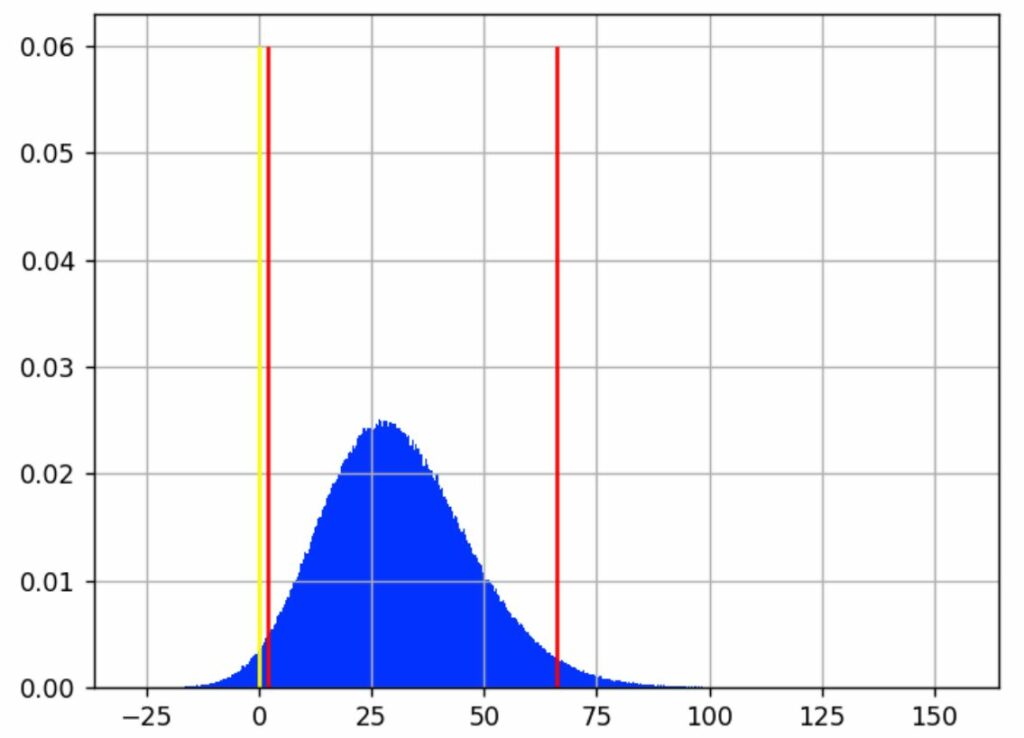
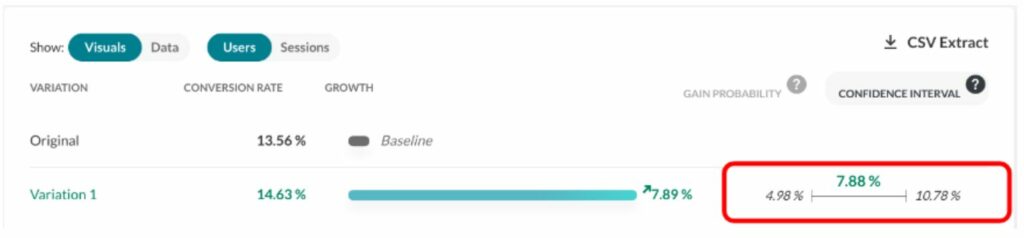
Wenn du AB Tasty als Experimentierplattform verwendest, erhältst du einen Bericht, der die „Gewinnchance“ zusammen mit anderen statistischen Informationen über deine Experimente enthält. Ein Bericht von AB Tasty enthält auch das Konfidenzintervall für den geschätzten Gewinn als wichtigen Indikator. Die Grenzen um den geschätzten Gewinn werden ebenfalls nach dem Bayesschen Prinzip berechnet, d. h. sie können als bestes und schlechtestes Szenario interpretiert werden.
Die Bedeutung der Bayesschen Statistik
Jetzt verstehest du die genaue Bedeutung des wohlbekannten 95 %-igen „Signifikanzniveaus“ und kannst geeignete Schwellenwerte für deinen speziellen Fall wählen.
Es ist wichtig, sich daran zu erinnern, dass dieser Ansatz nur mit der Bayesschen Statistik funktioniert, da frequentistische Ansätze statistische Indizes (wie p-Werte und Konfidenzintervalle) liefern, die eine völlig andere Bedeutung haben und für die erklärte Logik nicht geeignet sind.
2. Sind die Statistiken bei kleinen Zahlen gültig?
Ja, solange man den Test nicht abhängig vom Ergebnis abbricht.
Denke daran, dass laut Testprotokoll der einzige Grund für den Teststopp das Ende des Zeitrahmens ist. In diesem Fall sind die statistischen Indizes („Gewinnchancen“ und Konfidenzintervall) wahr und brauchbar.
Du denkst jetzt möglicherweise: „Okay, aber dann erreiche ich selten das Signifikanzniveau von 95 % …“
Vergiss nicht, dass der Schwellenwert von 95 % nicht in allen Fällen die magische Zahl sein muss. Bei einem geringen Traffic ist deine Website wahrscheinlich noch nicht alt. Wenn du dich auf den vorherigen Punkt beziehst, kannst du einen Blick auf unsere vorgeschlagene Skala für verschiedene Szenarien werfen.
Wenn du als neueres Unternehmen mit geringerem Traffic zu tun hast, kannst du sicherlich zu einem niedrigeren Schwellenwert (wie z. B. 90 %) wechseln. Der Schwellenwert ist immer noch höher, weil man in der Regel mehr Vertrauen in ein Original als in eine Variante hat, da sie schon länger verwendet wird.
Wenn es sich um zwei völlig neue Varianten handelt, ist es am Ende des Testzeitraums einfacher, die Variante mit den höheren Conversion Rates auszuwählen (ohne eine Statistik zu verwenden), da es kein Vorwissen über die Leistung von A oder B gibt.
3. Gehe „weiter nach oben“
Manchmal ist das Traffic-Problem nicht auf eine Website mit geringem Traffic zurückzuführen, sondern auf die betreffende Webseite. Normalerweise befinden sich Seiten mit geringem Traffic am Ende des Funnels.
In diesem Fall ist es eine gute Strategie, an der Optimierung des Funnels näher am Einstiegspunkt der Nutzer zu arbeiten. Möglicherweise gibt es mit einer optimierten digitalen Customer Journey noch mehr aufzudecken, bevor das Ende des Funnels erreicht wird.
4. Ist die CUPED-Technik real?
Was ist CUPED?
CUPED bzw. „Controlled Experiment Using Pre-Experiment Data“ ist ein neues Schlagwort in der Welt der Experimente. CUPED ist eine Technik, die angeblich bis zu 50 % schnellere Ergebnisse liefert. Für Websites mit geringem Traffic natürlich sehr verlockend.
Funktioniert CUPED wirklich so gut?
Nicht ganz, und zwar aus zwei Gründen: zum einen aus organisatorischen Gründen und zum anderen wegen der Anwendbarkeit.
Die organisatorische Einschränkung
Was oft vergessen wird, ist, dass CUPED für Controlled Experiment Using Pre-Experiment Data steht.
In der Praxis beträgt der ideale Zeitraum für „Daten vor dem Experiment“ zwei Wochen, um eine Zeitersparnis von 50 % zu erreichen.
Bei einem klassischen 2-Wochen-Test behauptet CUPED also, dass du den Test in nur einer Woche beenden kannst.
Um jedoch die Ergebnisse richtig einschätzen zu können, benötigst du zwei Wochen Daten aus der Zeit vor dem Experiment. Du musst also drei Wochen Zeit haben, um CUPED zu implementieren und die gleiche Genauigkeit wie bei einem klassischen 2-Wochen-Test zu erzielen.
Ja, du hast richtig gelesen. Letztendlich brauchst du drei Wochen, um das Experiment durchzuführen.
Das bedeutet, dass es nur dann sinnvoll ist, wenn du bereits zwei Wochen Traffic-Daten gesammelt hast, die nicht für Experimente genutzt werden. Selbst wenn du zwei experimentlose Wochen in die Planung deiner Experimente integrieren kannst, um Daten zu sammeln, wird dies den Traffic für andere Experimente blockieren.
Die Anwendbarkeitsbeschränkung
Zusätzlich zu der organisatorischen/2-wöchigen Zeitbeschränkung gibt es zwei weitere Voraussetzungen, damit CUPED effektiv ist:
- CUPED ist nur auf Besucher anwendbar, die durch die Website sowohl in der Zeit vor dem Experiment als auch währenddessen navigieren.
- Diese Besucher müssen dasselbe Verhalten hinsichtlich der zu optimierenden KPI zeigen. Die Daten der Besucher müssen zwischen den beiden Zeiträumen korrelieren.
Du wirst im folgenden Abschnitt sehen, dass CUPED durch diese beiden Einschränkungen für E-Commerce-Websites praktisch nicht möglich und nur für Plattformen anwendbar ist.
Kehren wir zu unserem Beispiel der Experimentiereinstellungen zurück:
- Zwei Wochen Daten aus der Zeit vor dem Experiment
- Zwei Wochen Experimentdaten (von denen wir hoffen, dass sie nur eine Woche dauern, da eine Zeitersparnis von 50 % erwartet wird)
- Das Optimierungsziel ist eine Transaktion: Erhöhung der Anzahl von Conversions.
Einschränkung Nr. 1 besagt, dass wir die gleichen Besucher vor dem Experiment und währenddessen haben müssen, aber die Customer Journey eines Users im E-Commerce dauert in der Regel nur etwa eine Woche.
Mit anderen Worten, die Wahrscheinlichkeit, dass dieselben Besucher in beiden Zeiträumen die Website besuchen, ist sehr gering. In diesem Zusammenhang ist nur ein sehr begrenzter Effekt von CUPED zu erwarten (bis hin zum Anteil der Besucher in beiden Zeiträumen).
Einschränkung Nummer 2 besagt, dass die Besucher das gleiche Verhalten hinsichtlich der Conversion (den zu optimierenden KPI) aufweisen müssen. Offen gestanden, diese Bedingung wird im E-Commerce einfach nie erfüllt.
Die Conversion im E-Commerce findet entweder während des Pre-Experiments oder während des Experiments statt, aber nicht bei beiden (es sei denn, deine Kunden kaufen häufig mehrmals während des Experimentierzeitraums ein).
Das bedeutet, dass es keine Chance gibt, dass die Conversions der Besucher zwischen den Zeiträumen korrelieren.
Zusammenfassend gesagt: CUPED ist zur Optimierung von Transaktionen auf Websites im E-Commerce einfach nicht geeignet.
In der wissenschaftlichen Originalarbeit wird dies klar hervorgehoben, aber der Beliebtheit halber wird diese Technik in der Testbranche falsch dargestellt.
Tatsächlich – und das ist in der wissenschaftlichen Literatur klar dargelegt – funktioniert CUPED nur bei mehrfachen Conversions für Plattformen mit wiederkehrenden Besuchern, die dieselben Aktionen durchführen.
Ausgezeichnete Plattformen für CUPED wären Suchmaschinen (wie Bing, auf der diese Technik erfunden wurde) oder Streaming-Plattformen, die User täglich besuchen und dieselben wiederkehrenden Aktionen ausführen (ein Video abspielen, auf einen Link in einer Suchergebnisseite klicken, usw.).
Selbst wenn du versuchst, eine Anwendung von CUPED für den E-Commerce zu finden, wirst du feststellen, dass dies nicht möglich ist.
- Man könnte versuchen, die Anzahl der gesehenen Produkte zu optimieren, aber das Problem von Einschränkung 1 bleibt bestehen: eine sehr geringe Anzahl von Besuchern wird in beiden Datensätzen vorhanden sein. Und es gibt noch einen noch fundamentaleren Einwand – dieser KPI sollte nicht allein optimiert werden, da du sonst möglicherweise dazu beiträgst, dass Besucher zwischen den Produkten zögern.
- Du kannst nicht einmal versuchen, die Anzahl der von den Besuchern bestellten Produkte mit CUPED zu optimieren, da die Einschränkung Nummer 2 immer noch gilt. Der Kauf kann als unverzüglich betrachtet werden. Daher kann er nur in dem einen oder in dem anderen Zeitraum stattfinden – nicht in beiden. Wenn keine Korrelation des Besucherverhaltens zu erwarten ist, ist auch kein CUPED-Effekt zu erwarten.
Schlussfolgerung über CUPED
CUPED eignet sich nicht für Websites im E-Commerce, bei denen eine Transaktion das Hauptziel der Optimierung ist. CUPED ist nicht dein Geheimrezept, das dir hilft, dein Unternehmen zu optimieren – es sei denn, du bist Bing, Google oder Netflix.
Diese Technik ist sicherlich ein Schlagwort, das schnell Interesse weckt, aber es ist wichtig, das Gesamtbild zu sehen, bevor man CUPED in seine Roadmap aufnimmt. Marken im E-Commerce sollten daran denken, dass diese Testtechnik nicht für ihr Unternehmen geeignet ist.
Optimierung für Websites mit geringem Traffic
Marken mit geringem Traffic sind immer noch erstklassige Kandidaten für die Website-Optimierung, auch wenn sie sich möglicherweise an einen anderen Ansatz anpassen müssen, der nicht so traditionell ist.
Ob die Optimierung deiner Webseiten bedeutet, eine Seite zu wählen, die im Funnel weiter oben anzutreffen ist, oder ob du eine etwas niedrigere Schwelle wählst – entscheidend ist, dass die Optimierung kontinuierlich verläuft.
Möchtest du mit der Optimierung deiner Website beginnen? AB Tasty ist die branchenführende Plattform zur Optimierung der User Experience, mit der du schnell für ein umfassenderes digitales Erlebnis sorgen kannst. Von Experimenten bis hin zur Personalisierung kann diese Lösung dir helfen, deine Zielgruppe zu aktivieren und sich zu engagieren, um deine Conversions zu steigern.