Die Debatte über die beste Methode zur Interpretation von Testergebnissen gewinnt in der Welt der Conversion Rate Optimierung zunehmend an Bedeutung.
Zwei inferenzstatistische Methoden (Bayessche vs. Frequentistische) lösen heftige Diskussionen darüber aus, welche die „beste“ sei. Bei AB Tasty haben wir beide Ansätze sorgfältig untersucht und für uns gibt es nur einen Gewinner.

Lassen Sie uns zunächst auf die Logik hinter den beiden Methoden eingehen und die wesentlichen Unterschiede sowie Vorteile beider Methoden untersuchen. In diesem Artikel greifen wir folgende Punkte auf:
[toc]
Was sind Hypothesentests?
Der Rahmen für statistische Hypothesentests bei digitalen Experimenten kann durch zwei gegenteilige Hypothesen ausgedrückt werden:
- H0 besagt, dass es keinen Unterschied zwischen dem Treatment (die bearbeitete Variante) und der Originalversion gibt. Mit anderen Worten: das Treatment hat keinen Einfluss auf den gemessenen KPI.
- H1 besagt, dass es einen Unterschied zwischen dem Treatment und der Originalversion gibt. Somit hat das Treatment also Einfluss auf den gemessenen KPI.
Ziel ist es, Indikatoren zu berechnen, die Ihnen anhand der experimentellen Daten bei der Entscheidung helfen, ob Sie das Treatment (im Kontext von AB Tasty eine Variante) beibehalten oder verwerfen sollen. Zunächst bestimmen wir die Anzahl der zu testenden BesucherInnen, sammeln die Daten und prüfen dann, ob die Variante besser als das Original abschneidet.

Im Wesentlichen gibt es zwei Ansätze für statistische Hypothesentests:
- Frequentistischer Ansatz: Vergleich der Daten mit einem Modell.
- Bayesscher Ansatz: Vergleich zweier Modelle (die aus Daten erstellt wurden).
Zur Durchführung des aktuellen Reportings und der Experimente, entschied sich AB Tasty vom ersten Moment an für den Bayesschen Ansatz.
Was ist der frequentistische Ansatz?
Bei diesem Ansatz erstellen wir ein Modell Ma für die Originalversion (A), die die Wahrscheinlichkeit P angibt, bestimmte Daten Da zu sehen. Es handelt sich dabei um folgende Funktion:
Ma(Da) = p
Dann können wir aus Ma(Db) einen p-Wert (Pv) errechnen. Dieser gibt die Wahrscheinlichkeit an, die bei Variante B gemessenen Daten zu sehen, wenn sie durch die Originalversion (A) erzeugt wurden.
Rein vom Gefühl her bedeutet ein hoher Pv, dass die bei B gemessenen Daten auch von A hätten produziert werden können (was die Hypothese H0 unterstützt). Ist Pv hingegen niedrig, bedeutet dies, dass die Wahrscheinlichkeit sehr gering ist, dass die bei B gemessenen Daten auch durch A hätten erzeugt werden können (was die Hypothese H1 unterstützt).
Ein weit verbreiteter Schwellenwert für Pv ist 0,05. Das heißt, damit die Variante einen Effekt hat, muss die Wahrscheinlichkeit unter 5 % liegen, dass die bei B gemessenen Daten auch von A stammen könnten.
Dieser Ansatz bietet den wesentlichen Vorteil, dass nur A modelliert werden muss. Dies ist interessant, da es sich um die ursprüngliche Variante handelt und diese schon länger als B existiert. Man könnte also durchaus glauben, dass man über einen langen Zeitraum Daten aus A sammeln kann, um aus diesen Daten ein genaues Modell zu erstellen. Leider bleibt der KPI, den wir beobachten, nur selten unverändert. Transaktionen oder Klickraten sind im Laufe der Zeit sehr variabel, weshalb man das Modell Ma erstellen und die Daten aus B im selben Zeitraum erheben muss, um einen gültigen Vergleich zu erhalten. Dieser Vorteil lässt sich offensichtlich nicht im Kontext digitaler Experimente anwenden.
Dieser Ansatz wird als „Frequentist“ bezeichnet, da er die Frequenz misst, in der bestimmte Daten wahrscheinlich bei einem bekannten Modell auftreten.
Wichtig ist darauf hinzuweisen, dass dieser Ansatz – wie wir oben gesehen haben – die beiden Prozesse nicht vergleicht.
Hinweis: Da p-Werte nicht intuitiv sind, werden sie oft wie folgt in eine Wahrscheinlichkeit umgewandelt:
p = 1-P-Wert
Häufig werden sie fälschlicherweise als die Wahrscheinlichkeit dargestellt, dass H1 wahr ist (was bedeutet, dass es einen Unterschied zwischen A und B gibt). Tatsächlich handelt es sich aber, um die Wahrscheinlichkeit, dass die bei B gesammelten Daten nicht von A erzeugt wurden.
Was ist der Bayessche Ansatz (den AB Tasty verwendet)?
Bei diesem Ansatz erstellen wir zwei Modelle, Ma und Mb (eines für jede Variante) und vergleichen sie dann. Diese Modelle, die auf der Grundlage von experimentellen Daten erstellt werden, erzeugen nach dem Zufallsprinzip die Stichproben: A und B. Wir verwenden diese Modelle, um Stichproben möglicher Raten zu erstellen und die Differenz zwischen diesen Raten zu berechnen. Mit dem Ziel, die Verteilung der Differenz zwischen den beiden Prozessen einzuschätzen.
Im Gegensatz zum ersten Ansatz, vergleicht dieser zwei Modelle miteinander. Hier spricht man vom Bayesschen Ansatz oder der Bayesschen Methode.
Nun müssen wir ein Modell für A und B erstellen.
Klicks können als Binomialverteilungen, mit den Parametern Anzahl der Versuche und Erfolgsquote, dargestellt werden. Bei digitalen Experimenten entspricht die Anzahl der Versuche der Anzahl der BesucherInnen und die Erfolgsquote der Klick- oder Transaktionsrate. In diesem Fall ist es wichtig zu wissen, dass es sich bei den uns betreffenden Raten nur um Schätzungen für eine begrenzte Anzahl von BesucherInnen handelt. Um diese begrenzte Genauigkeit zu modellieren, verwenden wir Beta-Verteilungen (entspricht der konjugierten a-priori-Verteilung von Binomialverteilungen).
Diese Verteilungen modellieren die Wahrscheinlichkeit einer Erfolgsquote, die bei einer begrenzten Anzahl von Versuchen gemessen wird.
Beispiel:
- 1.000 BesucherInnen bei A mit 100 Erfolgen
- 1.000 BesucherInnen bei B mit 130 Erfolgen
Wir erstellen das Modell Ma = beta(1+Erfolg_a,1+Misserfolge_a), wobei Erfolg_a = 100 & Misserfolge_a = BesucherInnen_a – Erfolg_a =900 ist.
Sicher haben Sie ein +1 für die Parameter Erfolg und Misserfolg bemerkt, was sich in der Bayesschen Analyse durch den „Prior“ erklären lässt. Ein Prior ist etwas, was Sie bereits vor dem Experiment kennen. Z.B. etwas, was aus einem anderen (früheren) Experiment abgeleitet wurde. Bei digitalen Experimenten ist jedoch gut dokumentiert, dass die Klickraten nicht gleichbleibend sind und sich je nach Tages- oder Jahreszeit ändern können. Folglich können wir dies in der Praxis nicht verwenden. Die entsprechende Prior-Einstellung +1 ist einfach ein nicht informativer Prior, da Sie auf keine vorherigen brauchbaren Experimentierdaten zurückgreifen können.
Bei den drei folgenden Diagrammen entspricht die horizontale Achse der Klickrate und die vertikale Achse der Wahrscheinlichkeit dieser Rate. Dabei ist bekannt, dass bei einem vorherigen Experiment 100 Erfolge bei 1.000 Versuchen verzeichnet wurden.
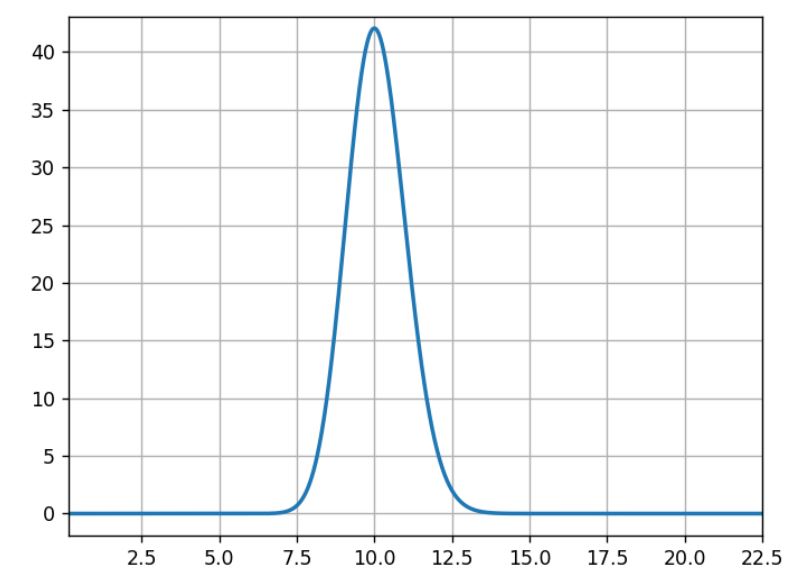
Normalerweise sind hier 10 % am wahrscheinlichsten, 5 % oder 15 % sehr unwahrscheinlich und 11 % halb so wahrscheinlich wie 10 %.
Das Modell Mb wird mit den Daten aus Versuch B auf die gleiche Weise erstellt:
Mb= beta(1+100,1+870)
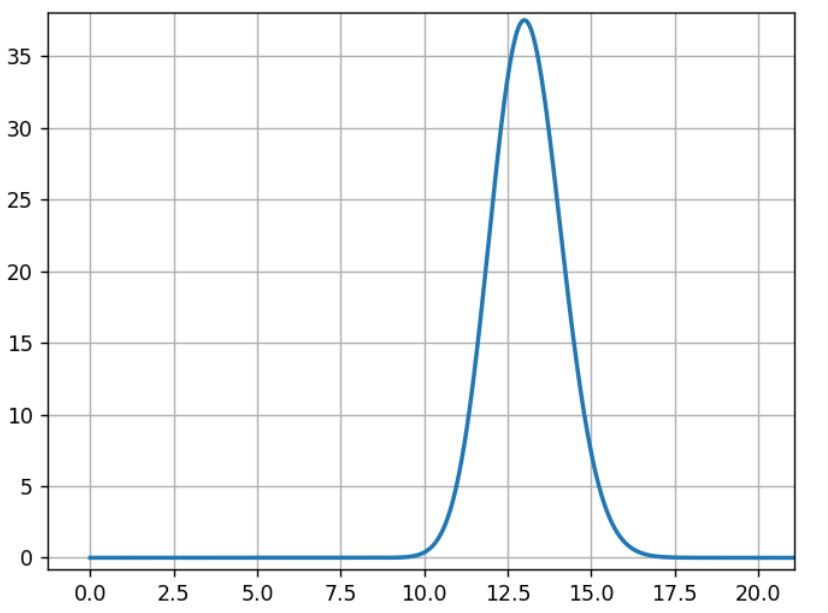
Für B liegt die wahrscheinlichste Rate bei 13 % während die Breite der Kurve ähnlich der vorherigen Kurve ist.
Nun vergleichen wir die Ratenverteilung von A und B.
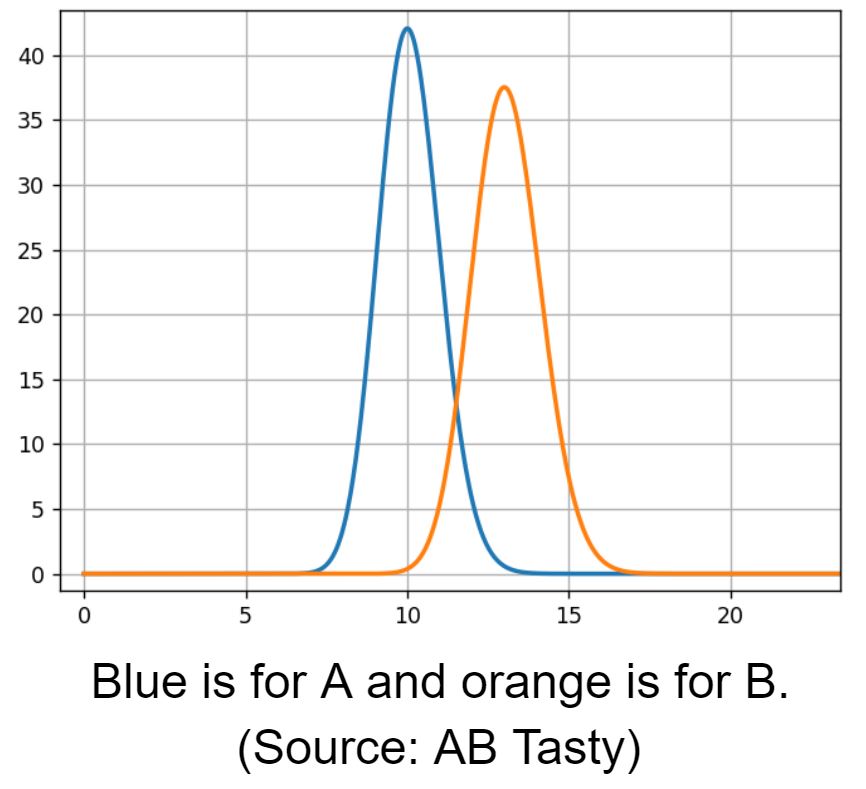
Wir sehen einen sich überlappenden Bereich bei einer Conversion Rate von 12 %. Hier haben beide Modelle die selbe Wahrscheinlichkeit. Für eine Schätzung des sich überlappenden Bereichs müssen wir aus beiden Modellen Stichproben ziehen und sie vergleichen.
Wir ziehen Stichproben aus den Verteilungen A und B:
- s_a[i] ist die Stichprobe i th aus A
- s_b[i] ist die Stichprobe i th aus B
Dann wenden wir eine Vergleichsfunktion auf diese Stichproben an:
- der relative Gewinn: g[i] =100* (s_b[i] – s_a[i])/s_a[i] für alle i.
Es handelt sich um die Differenz zwischen den möglichen Raten für A und B in Bezug auf A (multipliziert mit 100 für die Lesbarkeit in %).
Nun können wir die Stichproben g[i] mit einem Histogramm analysieren:
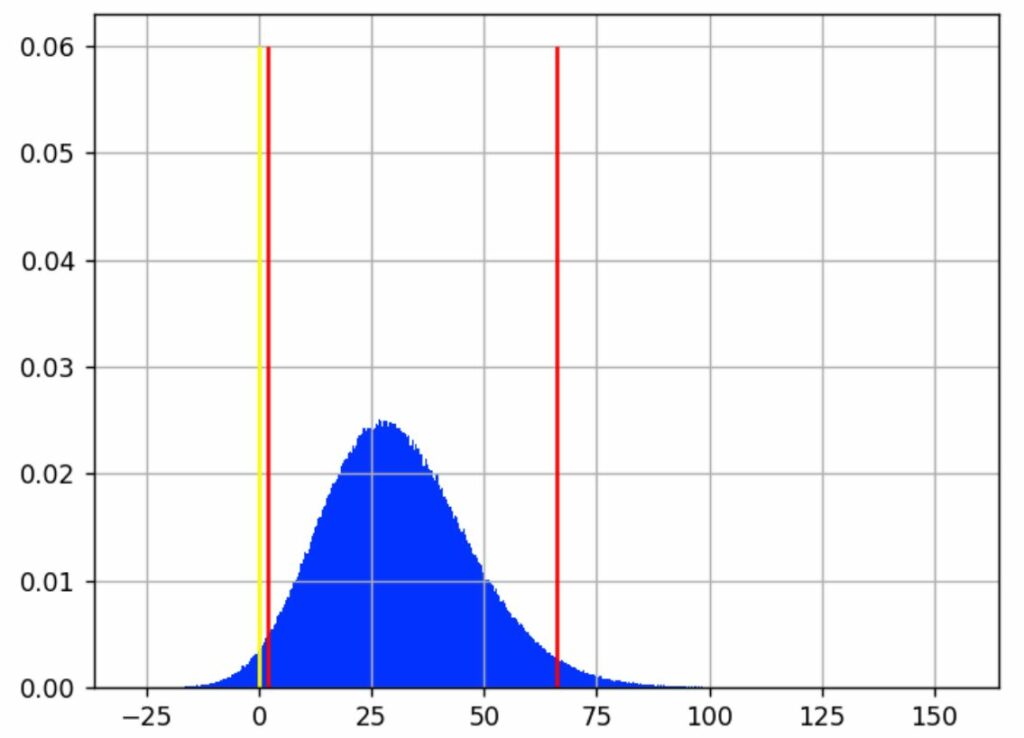
Wir sehen, dass der wahrscheinlichste Wert für den Gewinn bei rund 30 % liegt.
Die gelbe Linie zeigt, wo der Gewinn bei 0 liegt, d. h. es gibt keinen Unterschied zwischen A und B. Stichproben links von dieser Linie entsprechen Fällen, in denen A > B ist. Stichproben auf der anderen Seite sind Fälle, in denen A < B ist.
Anschließend definieren wir die Gewinnwahrscheinlichkeit wie folgt:
GW = (Anzahl der Stichproben > 0)/Gesamtanzahl der Stichproben
Bei 1.000.000 (10^6) Stichproben für g haben wir 982.296 Stichproben >0, sodass B>A ~ zu 98 % wahrscheinlich ist.
Wir nennen dies die „Gewinnchancen“ oder die „Gewinnwahrscheinlichkeit“ (die Wahrscheinlichkeit, dass man etwas gewinnt).
Die Gewinnwahrscheinlichkeit wird im Report hier dargestellt (siehe rotes Rechteck):
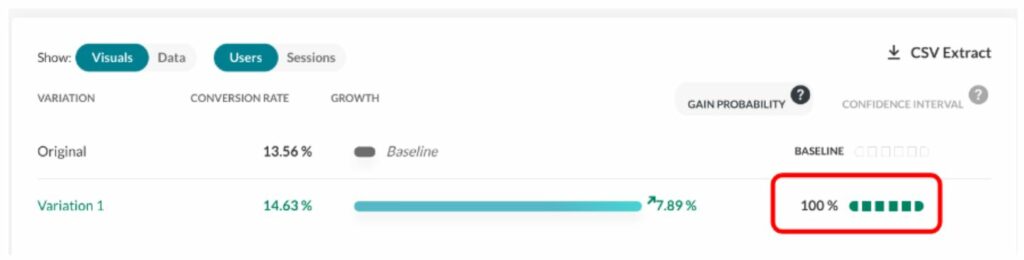
Mit der gleichen Stichprobenmethode können wir klassische Analysekennzahlen wie Mittelwert, Median, Perzentile usw. berechnen.
Bei Betrachtung des vorherigen Diagramms geben die roten vertikalen Linien an, wo sich der größte Teil des blauen Bereichs befindet, d. h. intuitiv, welche Gewinnwerte am wahrscheinlichsten sind.
Wir haben entschieden, ein Best Case- und ein Worst Case-Szenario mit einem Konfidenzintervall von 95 % zu präsentieren. Dabei wurden 2,5 % der Fälle im Extrembereich (beste und schlechteste Fälle) ausgeschlossen, sodass insgesamt 5 % der von uns als selten betrachteten Ereignisse unberücksichtigt bleiben. Dieses Intervall wird durch die roten Linien im Diagramm abgegrenzt. Wir gehen davon aus, dass der tatsächliche Gewinn (so, als wenn wir für die Messung eine unendliche Anzahl an BesucherInnen hätten) in 95 % der Fälle irgendwo in diesem Intervall liegt.
In unserem Beispiel liegt dieses Intervall bei [1,80 %, 29,79 %, 66,15 %], was bedeutet, dass es relativ unwahrscheinlich ist, dass der tatsächliche Gewinn unter 1,8 % liegt. Ebenso ist es relativ unwahrscheinlich, dass der Gewinn 66,15 % überschreitet. Und die Wahrscheinlichkeit ist gleichermaßen groß, dass die reelle Rate über oder unter dem Medianwert von 29,79 % liegt.
Das Konfidenzintervall wird im Report (eines anderen Experiments) hier dargestellt (siehe rotes Rechteck):
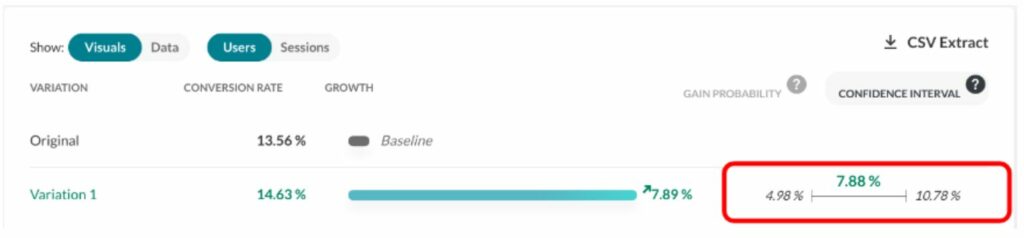
Was sind „Prior“ beim Bayesschen Ansatz?
In Bayesschen Frameworks wird der Begriff „Prior“ für die Informationen verwendet, über die Sie vor dem Experiment verfügen. Ein Beispiel: Allgemein ist bekannt, dass die Transaktionsrate im e-Commerce in den meisten Fällen unter 10 % liegt.
Es wäre sehr interessant gewesen, diesen Punkt einzubinden, aber diese Vermutungen sind in der Praxis schwer anzustellen, da die Saisonalität der Daten einen großen Einfluss auf die Klickraten hat. Tatsächlich liegt hier der Hauptgrund, weshalb wir die Daten für A und B gleichzeitig erheben. Meistens liegen uns bereits vor dem Experiment Daten von A vor. Wir wissen jedoch, dass sich die Klickraten im Laufe der Zeit ändern, sodass wir die Klickraten im Hinblick auf einen gültigen Vergleich für alle Varianten gleichzeitig erheben müssen.
Daraus folgt, dass wir einen nicht-informativen Prior verwenden müssen. Das bedeutet, dass wir vor dem Experiment nur wissen, dass die Raten zwischen [0 %, 100 %] liegen. Wir wissen nicht, wie hoch der Gewinn ausfallen kann. Dieselbe Vermutung wie beim Frequentistischen Ansatz, auch wenn sie nicht formuliert wurde.
Herausforderungen bei statistischen Tests
Wie bei jedem Testansatz wird auch hier das Ziel gesetzt, Fehler auszuschalten. Es gibt zwei Arten von Fehlern, die Sie vermeiden sollten:
- Falsch positiv (FP): Wenn Sie eine Gewinnervariante auswählen, die in Wirklichkeit nicht die Variante mit der besten Performance ist.
- Falsch negativ (FN): Wenn Sie eine Gewinnervariante verpassen. Entweder deklarieren Sie am Ende des Experiments keinen Gewinner oder den falschen Gewinner.
Die Performance bei beiden Messungen hängt vom verwendeten Schwellenwert (p-Wert oder Gewinnwahrscheinlichkeit) ab, der wiederum vom Kontext des Experiments abhängt. Die Entscheidung muss der oder die NutzerIn treffen.
Ein weiterer wichtiger Parameter ist die Anzahl der für das Experiment herangezogenen BesucherInnen, da sie einen starken Einfluss auf die falsch negativen Fehler hat.
Aus geschäftlicher Sicht ist ein falsch negatives Ergebnis eine verpasste Chance. Bei der Reduzierung falsch negativer Fehler geht es hauptsächlich um die Größe der Population, die dem Test zugewiesen ist: im Grunde genommen geht es darum, dem Problem mehr Besucher zuzuführen.
Das Hauptproblem sind allerdings falsch positive Ergebnisse, die hauptsächlich in zwei Situationen auftreten:
- Bereits sehr früh im Experiment: Bevor die angestrebte Stichprobengröße erreicht ist, wenn die Gewinnwahrscheinlichkeit höher als 95 % ist. Es passiert, dass NutzerInnen zu ungeduldig sind und zu schnell Schlüsse ziehen, ohne dass genügend Daten vorliegen; das Gleiche gilt für falsch positive Ergebnisse.
- Sehr spät im Experiment: Wenn die angestrebte Stichprobengröße erreicht ist, aber kein signifikanter Gewinner gefunden wird. Manche UserInnen glauben zu sehr an ihre Hypothese und wollen ihr eine weitere Chance geben.
Beide Probleme können durch strikte Einhaltung des Testprotokolls vermieden werden, indem Sie einen Testzeitraum mit einem Stichprobenrechner festlegen und sich daran halten.
Bei AB Tasty gibt es eine visuelle Markierung mit dem Namen „Readiness“. Sie zeigt an, ob Sie sich an das Protokoll halten (ein Zeitraum von mindestens 2 Wochen und mindestens 5.000 BesucherInnen). Bei jeder Entscheidung über diese Richtlinien hinaus sollten die im nächsten Abschnitt beschriebenen Regeln beachtet werden, um das Risiko falsch positiver Ergebnisse zu reduzieren.
Dieser Screenshot zeigt, wie UserInnen darüber informiert werden, ob Maßnahmen ergriffen werden können.
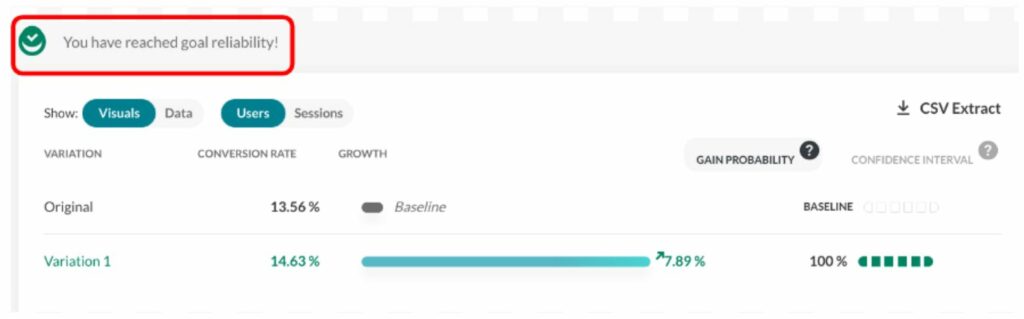
Während des Zeitraums der Datenerhebung sollte man im Report lediglich prüfen, ob die Erhebung korrekt ist (ohne Häkchen bei „Zuverlässigkeit“) und nur nach extremen Fälle suchen, bei denen sofort gehandelt werden muss. Geschäftliche Entscheidungen aber sollten noch nicht getroffen werden.
Wann sollten Sie Ihr Experiment abschließen?
Early Stop
Bei einem „Early Stop“ möchte ein Nutzer oder eine Nutzerin einen Test stoppen, bevor die zugewiesene Anzahl der BesucherInnen erreicht ist.
Der oder die NutzerIn sollte warten, bis die Kampagne mindestens 1.000 BesucherInnen erreicht hat, und erst bei besonders hohen Verlusten abbrechen.
Wenn ein Nutzer oder eine Nutzerin für eine vermeintliche Gewinnervariante vorzeitig aufhören möchte, sollte mindestens zwei Wochen gewartet und nur Daten einer vollständigen Woche genutzt werden. Diese Taktik ist dann interessant, wenn die Geschäftskosten eines falsch positiven Ergebnisses noch in Ordnung sind. Dann ist es wohl wahrscheinlicher dass die Performance der vermeintlichen Gewinnervariante ähnlich zu der des Original ist, als dass ein Verlust entsteht.
Nochmals: Wenn dieses Risiko aus geschäftsstrategischer Sicht akzeptabel ist, ist diese Taktik sinnvoll.
Wenn ein(e) UserIn zu Beginn eines Tests eine Gewinnervariante (mit einer hohen Gewinnwahrscheinlichkeit) sieht, sollte für das Worst Case-Szenario eine Marge sichergestellt werden. Eine untere Grenze für den Gewinn nahe 0 % kann sich durchaus ändern und am Ende des Tests unter oder weit unter null liegen, was die anfangs angenommene hohe Gewinnwahrscheinlichkeit untergräbt. Die Vermeidung eines vorzeitigen Abbruchs mit einer niedrigen linken Konfidenzgrenze trägt dazu bei, falsch positive Ergebnisse zu Beginn eines Tests auszuschließen.
Beispielsweise ist eine Situation mit einer Gewinnwahrscheinlichkeit von 95 % und einem Konfidenzintervall wie [-5,16 %, 36,48 %, 98,02 %] ein Merkmal für einen vorzeitigen Abbruch. Die Gewinnwahrscheinlichkeit liegt über dem akzeptierten Standard, weshalb man vielleicht also 100 % des Traffics auf die Gewinnvariante leiten möchte. Das Worst Case-Szenario (-5,16 %) liegt jedoch relativ weit unter 0 %, was auf ein mögliches falsch positives Ergebnis hindeutet und somit auf jeden Fall riskant ist. Denn im Worst Case-Szenario gehen 5 % der Conversions verloren. Besser ist es so lange zu warten, bis die untere Grenze des Konfidenzintervalls bei mindestens >0 % liegt. Eine kleine Marge darüber wäre noch sicherer.
Später Abbruch
Bei einem „späten Abbruch“ lässt man am Ende eines Tests den Test länger als ursprünglich geplant laufen, da keine signifikante Gewinnervariante gefunden wurde. Der Nutzer oder die Nutzerin vertritt dabei die Hypothese, dass der Gewinn kleiner als erwartet ausfällt und für eine signifikante Aussage mehr BesucherInnen benötigt werden.
Wenn man entscheidet, ob die Laufzeit des Tests verlängert werden soll, ohne dem Protokoll zu folgen, sollte eher das Konfidenzintervall statt die Gewinnwahrscheinlichkeit berücksichtigt werden.
Wer Tests länger als geplant durchführen möchte, dem raten wir, nur sehr vielversprechende Tests zu verlängern. Dies bedeutet, einen hohen Wert für das beste Szenario zu haben (die rechte Grenze des Konfidenzintervalls sollte hoch sein).
Zum Beispiel ist dieses Szenario mit einer Gewinnwahrscheinlichkeit von 99 % und einem Konfidenzintervall von [0,42 %, 3,91 %] typisch für einen Test, der nicht über seine geplante Dauer hinaus verlängert werden sollte: Eine große Gewinnwahrscheinlichkeit, aber kein hohes Best Case-Szenario (nur 3,91 %).
Beachten Sie, dass sich das Konfidenzintervall mit zunehmender Stichprobenzahl verkleinert. Das heißt, wenn es am Ende tatsächlich eine Gewinnervariante gibt, wird ihr Best Case-Szenario wahrscheinlich kleiner als 3,91 % sein. Lohnt sich das wirklich? Wir raten, zum Stichprobenrechner zurückzukehren und zu sehen, wie viele BesucherInnen für eine solche Genauigkeit erforderlich sind.
Hinweis: Diese Zahlenbeispiele stammen aus einer Simulation von A/A-Tests, wobei ein gescheiterter Test ausgewählt wurden.
Die Lösung: Konfidenzintervalle
Die Verwendung des Konfidenzintervalls anstelle der alleinigen Betrachtung der Gewinnwahrscheinlichkeit wird die Entscheidungsfindung erheblich verbessern. Ganz zu schweigen davon, dass dies unabhängig vom Problem falsch positiver Ergebnisse geschäftlich wichtig ist. Alle Varianten müssen die Kosten für die Umsetzung in der Produktion decken. Man darf nicht vergessen, dass die Originalversion bereits besteht und keine zusätzlichen Kosten verursacht. Daher tendiert man implizit und pragmatisch immer zum Original.
Jede Optimierungsstrategie sollte einen minimalen Schwellenwert für die Größe des Gewinns haben.
Eine andere Art von Problem kann auftreten, wenn mehr als zwei Varianten getestet werden. In diesem Fall wird eine Holm-Bonferroni-Korrektur angewendet.
Warum AB Tasty den Bayesschen Ansatz gewählt hat
Zusammengefasst, was ist nun besser? Die Bayessche oder die frequentistische Methode?
Wie bereits gesagt: beide statistischen Methoden sind tragfähig. AB Tasty hat sich aus den folgenden Gründen für das Bayessche Statistikmodell entschieden:
- Verwendung eines Wahrscheinlichkeitsindexes, der eher dem entspricht, was die Nutzer und Nutzerinnen denken, statt eines p-Werts oder eines verschleierten Werts
- Bereitstellung von Konfidenzintervallen für fundiertere Geschäftsentscheidungen (nicht alle Gewinnervarianten sind wirklich interessant, um sie in die Produktion zu bringen). Ebenfalls ein Mittel, um falsch positive Fehler zu reduzieren.
Im Endeffekt ergibt es einen Sinn, dass die frequentistische Methode ursprünglich von so vielen Unternehmen übernommen wurde. Am Ende handelt es sich um eine Standardlösung, die leicht zu codieren und in jeder Statistikbibliothek zu finden ist (ein besonders wichtiger Vorteil, da die meisten EntwicklerInnen keine Statistiker sind).
Dennoch, auch wenn diese Methode anfangs für Experimente großartig war, gibt es heute bessere Möglichkeiten: die Bayessche Methode. Alles hängt davon ab, was Ihnen diese Möglichkeiten bieten: Während die frequentistische Methode zeigt, ob es einen Unterschied zwischen A und B gibt, geht die Bayessche Methode einen Schritt weiter und berechnet, wie groß der Unterschied ist.
Kurzum, bei Durchführung eines Experiments haben Sie bereits die Werte für A und B. Nun möchten Sie herausfinden, welchen Gewinn Sie erzielen, wenn Sie von A zu B wechseln. Diese Frage lässt sich am besten mit einem Bayesschen Test beantworten.





