Avez-vous déjà fait vos courses dans un supermarché et abandonné votre panier en plein milieu des rayons ? Non, évidemment personne ne fait ça ! Pourtant, nous avons tous déjà sélectionné des articles sur un site e-commerce que nous n’avons jamais acheté.
L’abandon de panier est un terrible fléau qui touche uniquement les e-commerçants. Ce phénomène « 100% web » reste encore très difficile à cerner… Pourtant, il a un impact considérable sur le taux de conversion ainsi que sur la rentabilité des achats en ligne. Que faire en cas d’abandon de panier ? Faut-il s’inquiéter ? Comment y mettre fin ?
Ne paniquez pas ! Pour y remédier, vous devez commencer par prendre du recul afin de comprendre les raisons qui poussent vos clients web à ne pas finaliser leurs achats. Avec une telle analyse, vous serez en mesure d’arranger cela rapidement !
Qu’est-ce que l’abandon de panier et comment le calculer ?
Commençons par une définition de l’abandon de panier. Il s’agit simplement du comportement de l’internaute consistant à visiter votre site, consulter vos pages produits, en mettre un ou plusieurs au panier, mais sans finaliser la commande. Vous pouvez calculer votre taux d’abandon de panier avec la formule suivante :
1 – (nombre de transactions/nombre de créations de panier)
Vous avez concrètement 2 options pour calculer ce taux d’abandon de panier :
- Mesurer précisément le nombre de créations de panier à l’aide d’un tracking spécifique d’évènement fourni par votre solution web analytics.
- Vous rabattre sur un autre indicateur si vous n’avez pas l’information précédente : le taux de conversion de votre tunnel d’achat depuis la page de récapitulatif panier, qui est bien souvent la 1re étape de votre tunnel. Le graphique ci-dessous est un exemple de tunnel configuré avec Google Analytics, le taux d’abandon de panier y est calculé en prenant comme dénominateur le nombre de visites avec affichage de la page de résumé du panier.
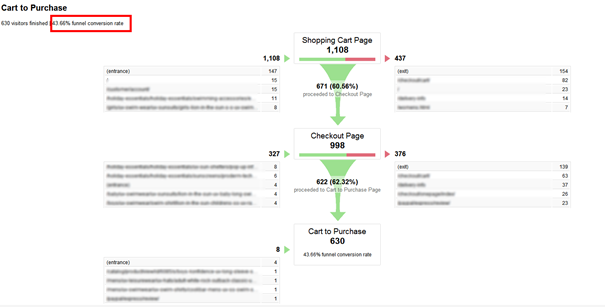
Nous préférons le 1er mode de calcul plus exhaustif, car les internautes qui abandonnent leur panier ne vont pas toujours jusqu’à consulter cette page récapitulative, sauf si vous les y forcez en les renvoyant directement vers cette page après chaque mise au panier. La tendance actuelle étant plutôt à la notification dynamique de mise au panier, tout en restant sur la page produit, les internautes qui abandonnent leur panier ne voient pas systématiquement cette page récapitulative. Pensez à bien dissocier l’abandon de panier, de l’abandon de tunnel.
Une fois cet indicateur calculé, vous pourrez alors comparer la performance de votre site avec la moyenne des e-commerçants. Vous pouvez également être intéressé par la valeur de votre panier moyen et comment l’augmenter.
Les chiffres clés de l’abandon de panier
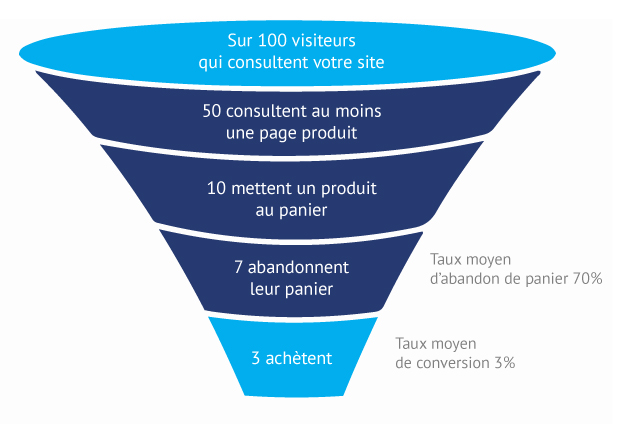
Le taux d’abandon de panier calculé précédemment a certainement de quoi vous effrayer, mais sachez que l’abandon de panier est un comportement très fréquent. On l’estime aux alentours de 68.53% (source : Baymard Institute, un institut d’études anglais indépendant). Il s’agit d’une moyenne issue de plus de 30 études différentes au cours des 10 dernières années. Qui plus est, ce taux a tendance à augmenter au fil des années, les études les plus récentes citant des taux avoisinant les 75% tous secteurs confondus.
Imaginez si 7 acheteurs sur 10 ayant rempli leur caddie en supermarché s’en aller en le laissant devant les caisses ! Si une forme de contrat social/moral empêche un tel comportement en points de vente physiques, il n’en est rien sur les sites de e-commerce où vos prospects ne sont en rien contraints.
7 internautes sur 10 mettant un de vos produits dans leur panier ne finaliseraient donc pas leur transaction. De quoi vous donner des sueurs froides… Surtout si vous mettez en parallèle ce chiffre avec celui du taux moyen d’achat au panier, de l’ordre de 9% seulement (source : emarketer). Pour enfoncer le clou, d’autres études ont cherché à quantifier le manque à gagner que représente l’abandon de panier. La dernière approximation de Forrester Research évalue à 18 000 milliards de dollars US les pertes chaque année, un chiffre qui devrait continuer à progresser à mesure que le e-commerce et le m-commerce se développent.
L’abandon de panier : une opportunité à saisir !
Si ces chiffres sont élevés, ils ne doivent pas vous paraître alarmistes. Bien que le taux d’abandon de panier soit un indicateur utile à piloter, surtout si vous entreprenez des actions d’optimisation de votre tunnel de commande, il ne résume pas à lui seul le processus de décision d’achat de l’internaute. Des études montrent en effet que même si la transaction n’est pas finalisée, l’ajout au panier traduit une intention. Autrement dit, un panier abandonné n’est pas automatiquement synonyme d’une vente perdue. Une étude de Seewhy (rachetée depuis par Hybris) révèle que ¾ des internautes ayant abandonné leur panier lors de la première visite prévoyaient de revenir sur le site ou en magasin soit pour réaliser un achat ferme, soit pour continuer leurs recherches qui conduiront éventuellement à un nouvel abandon de panier…
Cela est révélateur de la complexité du processus de décision d’achat, qui prend également du temps comme l’atteste cette même étude qui révèle que seulement 1% des visiteurs de votre site achètent lors de leur 1re visite et qu’il faut en moyenne 5 points de contact avant que l’internaute ne se décide à acheter. C’est pourquoi, plutôt que de considérer l’abandon de panier comme une malédiction, il faut le voir comme une opportunité, un premier moyen de jauger de l’intention de vos internautes.
En conclusion, si certains abandons de panier peuvent indiquer une insatisfaction vis-à-vis de votre offre, de vos produits et de vos services, d’autres sont simplement le signe précurseur d’une intention qui pourra se manifestera en achat en magasin ou en visites ultérieures. Les 3ème et 4ème billets de cette série couvriront justement ces 2 aspects :
- Comment optimiser vos pages produits et votre tunnel de conversion pour limiter les abandons résultants de défauts de conception ou d’ergonomie ?
- Comment concrétiser les intentions d’achat qui se cachent derrière certains abandons, notamment via les techniques de réactivation (display retargeting, email retargeting) ?
Grâce à ces conseils pratiques, vous ne ferez plus partie des 81% de responsables e-commerce qui considèrent qu’il est inutile de consacrer plus de temps aux internautes qui ne finalisent pas leur transaction. Mais avant d’aborder ces conseils, il nous parait nécessaire de rappeler les principales raisons de l’abandon de panier, car selon les symptômes les remèdes ne seront pas les mêmes…
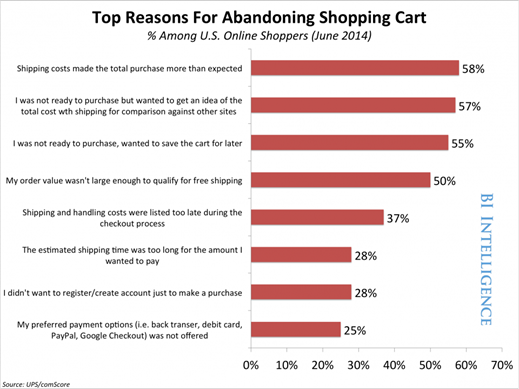
Plusieurs études se sont penchées sur les raisons de ce comportement et, bien que leurs résultats ne soient pas tous identiques, les mêmes éléments ressortent à divers degrés. Après avoir interrogé un panel d’internautes ayant abandonné leur panier sur un site e-commerce, eMarketer a mis en évidence 5 principales raisons. Parmi ceux ayant abandonné leur panier :
- 57% ont déclaré ne pas être prêt à acheter, mais simplement vouloir avoir une idée du coût global incluant les frais de livraison.
- 56% ont déclaré ne pas être prêt à acheter, mais simplement vouloir sauvegarder leur panier pour plus tard.
- 55% ont considéré que le total, en incluant les frais de livraison, était trop important.
- 51% ont déclaré que le montant de leur commande ne les rendait pas éligibles aux frais de livraison offerts.
- 40% ont considéré avoir une mauvaise surprise en découvrant les frais de livraison trop tard dans le tunnel de commande.
Les résultats de cette étude mettent en avant 2 points intéressants :
- Le rôle du panier d’achat n’est pas forcément celui qu’on croit. Alors que beaucoup d’e-commerçants considèrent le panier comme la première étape de leur tunnel de conversion, pour les internautes, il a souvent une tout autre fonction : il fait office de liste d’achat à conserver pour plus tard ou de moyen de comparer les prix en incluant les frais de livraison. Ce qui amène à repenser complètement le fonctionnement du panier d’achat en y incluant d’autres fonctionnalités.
- Le rôle des frais de livraison est capital. Très clairement, le montant des frais de livraison, l’absence de mention de ces frais ou leur apparition tardive dans le tunnel de décision sont des freins majeurs à la conversion. Les masquer volontairement dans l’espoir d’amener l’internaute plus en avant dans le tunnel de conversion n’est pas une stratégie viable et se paie d’une façon ou d’une autre plus tard.
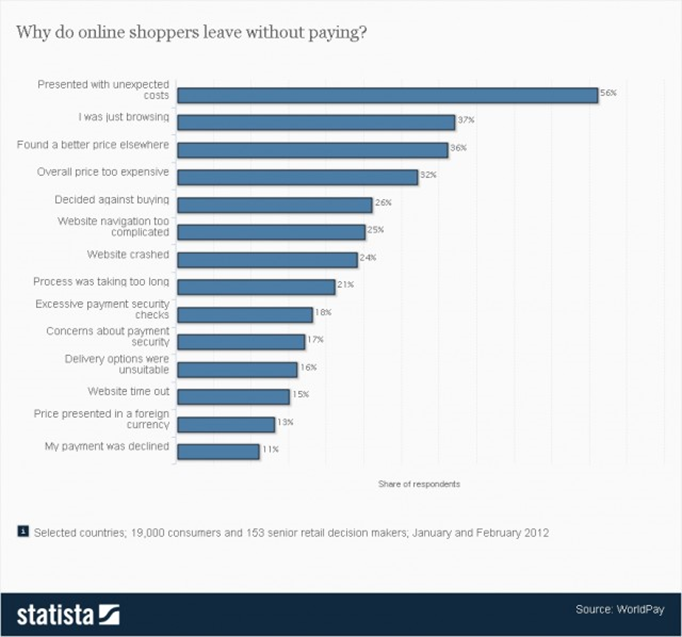
D’autres études, comme Statista, mettent en avant des points similaires ainsi que d’autres sources de friction, principalement liées à des problèmes d’utilisabilité même si ces derniers ne sont pas considérés comme une source majeure d’abandon de panier. Parmi ces facteurs, on notera des processus d’achat trop compliqués ou trop longs, nécessitant parfois la création d’un compte utilisateur, des problèmes d’ordre technique ou une confiance insuffisante dans la sécurité ou les garanties offertes par l’e-commerçant.
Comment limiter l’abandon de panier?
Il est maintenant temps de passer aux conseils pratiques. L’objectif est de pallier aux principaux défauts de conception et de s’assurer un processus de commande le plus fluide possible pour limiter les abandons de panier de personnes prêtes à acheter, mais qui ont renoncé du fait de problèmes rencontrés sur votre site.
1. Offrez les frais de livraison
Comme mentionné dans notre billet sur les raisons de l’abandon de panier, les frais de livraison constituent un frein majeur à la conversion. Une étude Forrester Research révèle que 40% des internautes qui abandonnent leur panier le font, car les frais de livraison ne sont pas offerts. TechCrunch relève également que 50% des sites e-commerce proposent aujourd’hui une livraison gratuite sous une forme ou une autre. Compte tenu du niveau de maturité et de concurrence de certains acteurs, comme Amazon, les internautes s’attendent à une livraison gratuite. Qui plus est, d’autres études ont montré que les internautes dépensés en moyenne 30% de plus lorsque les frais de livraison étaient offerts.
Donc, dans la mesure du possible prenez à votre charge les frais de livraison ou proposez des moyens de retraits qui donnent l’impression à l’internaute que la livraison ne lui coutera rien (ex : livraison en point retrait à proximité du domicile, click and collect, etc.).
Si vous ne pouvez pas offrir les frais de livraison toute l’année, organisez des périodes promotionnelles où vous ferez un effort particulier. Une étude UPS montre notamment que les commerçants qui offrent de temps en temps les frais de livraison voient leurs ventes grimper de 10 à 20% à ces périodes. Une autre possibilité est d’offrir les frais de livraison à partir d’un certain montant de commande pour maintenir une marge décente, augmenter son panier moyen, et faciliter le passage à l’acte de l’internaute motivé par vos produits. Une dernière alternative, si vous ne pouvez pas offrir les frais de livraison, consiste à proposer à l’internaute des incentives sous une forme ou une autre qui valoriseront son achat et feront passer la pilule des frais de livraison. Il peut s’agir d’un programme de fidélité, d’un bon de réduction pour un achat ultérieur, d’échantillons gratuits, etc.
2. Soyez transparent dès le début sur les frais de livraison
Les internautes veulent simplement savoir combien ils devront payer au total avant de se lancer dans votre tunnel de commande. Pour rappel, 37% des internautes qui ne finalisent pas leur transaction citent la découverte des frais de livraison tardivement comme la principale raison de leur abandon. Donc, plutôt que d’afficher les frais de livraison après s’être créé un compte, mentionnez-les le plus tôt possible. Il en va de même pour les taxes. Mentionnez toujours le prix toutes taxes comprises pour ne pas créer une désagréable surprise pour les internautes. 56% d’entre eux abandonnent en effet leur panier si l’e-commerçant leur présente des frais inattendus.
Le zoning de votre page produit est, à ce titre, capital. Vous devriez toujours indiquer le prix TTC et le montant des frais de livraison sur ce template de page. Si vous êtes en mesure d’offrir les frais de livraison, martelez-le également, à l’image de Sarenza. C’est un élément déterminant.
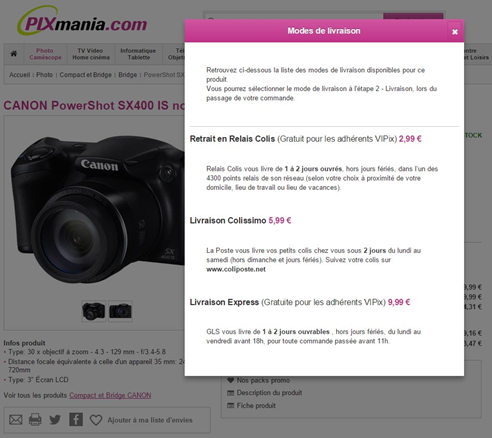
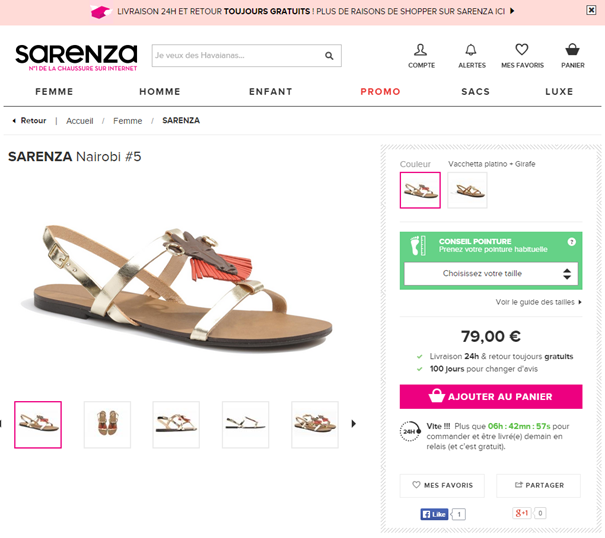 Vous pouvez aussi à l’instar de Pixmania, afficher les frais de livraison les moins chers (frais de livraison à partir de…) et un détail des options de livraisons avec les différents tarifs au survol de la souris. Notez également les frais de livraison expresse gratuits à partir du moment où l’internaute est membre du club VIPix et qui fait écho à un point évoqué précédemment : les incentives et programme de fidélité.
Vous pouvez aussi à l’instar de Pixmania, afficher les frais de livraison les moins chers (frais de livraison à partir de…) et un détail des options de livraisons avec les différents tarifs au survol de la souris. Notez également les frais de livraison expresse gratuits à partir du moment où l’internaute est membre du club VIPix et qui fait écho à un point évoqué précédemment : les incentives et programme de fidélité.
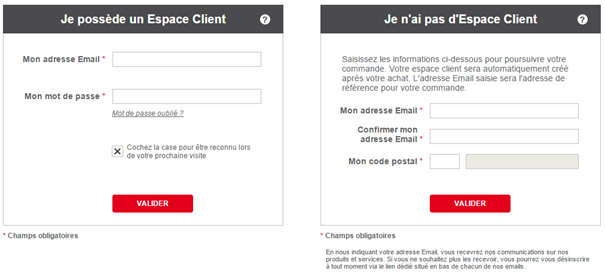
3. N’imposez pas la création d’un compte utilisateur pour pouvoir acheter
L’inscription sur un site est cause de l’abandon de panier dans 28% des cas. Se créer un compte rallonge en effet le processus de commande et impose une contrainte dès le début de celui-ci. Forcer les internautes à se créer un compte peut être synonyme de barrière comme le prouve une étude (User Interface Engineering) qui a démontré que supprimer la phase de création obligatoire d’un compte permettait d’augmenter de 45% le taux de conversion de certains e-commerçants.
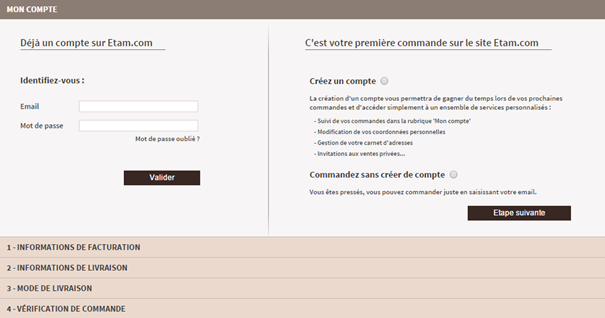
 Pour autant, la création d’un compte répond peut-être à d’autres objectifs marketing ou contraintes et s’avère dans certains cas indispensable. Heureusement, plusieurs alternatives sont envisageables. À l’instar d’Etam, vous pouvez rendre l’inscription facultative en rappelant néanmoins les bénéfices de se créer un compte (suivi des commandes, invitations aux ventes privées…). Vous satisfaisiez ainsi le plus grand nombre, aussi bien ceux qui ne souhaitent pas s’inscrire que ceux pour qui cela est indifférent ou au contraire ceux qui trouvent cela valorisant dans une logique de club ou de programme de fidélité.
Pour autant, la création d’un compte répond peut-être à d’autres objectifs marketing ou contraintes et s’avère dans certains cas indispensable. Heureusement, plusieurs alternatives sont envisageables. À l’instar d’Etam, vous pouvez rendre l’inscription facultative en rappelant néanmoins les bénéfices de se créer un compte (suivi des commandes, invitations aux ventes privées…). Vous satisfaisiez ainsi le plus grand nombre, aussi bien ceux qui ne souhaitent pas s’inscrire que ceux pour qui cela est indifférent ou au contraire ceux qui trouvent cela valorisant dans une logique de club ou de programme de fidélité.
Une autre option, plus insidieuse, mais tout aussi efficace, est de créer un compte automatiquement à l’internaute sans la présenter comme une étape en soi. Concrètement, il vous suffit, au moment où il renseigne ses coordonnées (nom, email, adresse…), de lui demander un simple mot de passe. Il aura conscience de se créer un compte, mais sera déjà suffisamment engagé dans votre tunnel de commande pour renoncer et surtout il n’aura pas à faire face à cette étape à part entière.
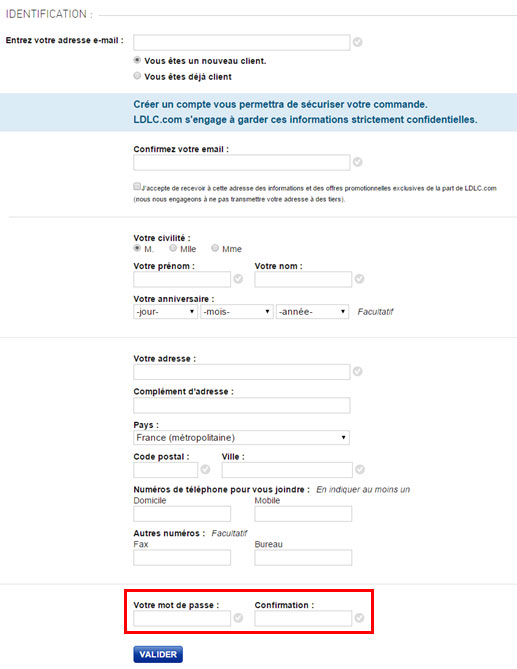 Une dernière possibilité consiste à demander la création du compte à l’issue de l’achat. Il sera alors plus facile d’inciter l’internaute à remplir cette étape, en lui rappelant que cela permettra notamment de suivre l’état de sa commande, d’accéder plus facilement au service support, etc.
Une dernière possibilité consiste à demander la création du compte à l’issue de l’achat. Il sera alors plus facile d’inciter l’internaute à remplir cette étape, en lui rappelant que cela permettra notamment de suivre l’état de sa commande, d’accéder plus facilement au service support, etc.
4. Limitez le nombre d’étapes de votre tunnel de commande
21% des internautes qui abandonnent leur panier le font, car ils considèrent le processus de commande trop long. Avez-vous testé de réduire le nombre d’étapes de votre tunnel ou un tunnel en une seule étape, aussi appelé « one-step-checkout » ?
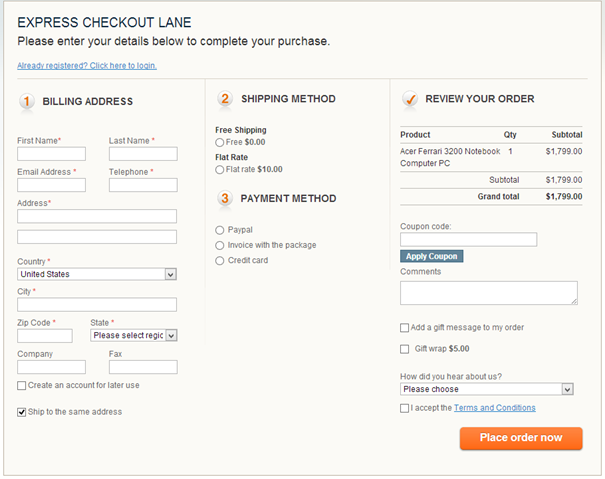 Attention toutefois, si certains tests ont montré une efficacité supérieure de ce type de tunnel donnant à l’internaute l’impression d’un processus plus court, d’autres ont démontré l’inverse, car moins d’information est demandée à chacune des étapes qui apparaissent alors plus simples à remplir. Chaque site étant différent, il faut tester ce qui convient le mieux à votre audience. Si vous optez pour plusieurs étapes, prenez soin de rappeler à l’internaute le nombre d’étapes auquel il doit s’attendre à l’aide d’une barre de progression et limitez à 3 le nombre d’étapes.
Attention toutefois, si certains tests ont montré une efficacité supérieure de ce type de tunnel donnant à l’internaute l’impression d’un processus plus court, d’autres ont démontré l’inverse, car moins d’information est demandée à chacune des étapes qui apparaissent alors plus simples à remplir. Chaque site étant différent, il faut tester ce qui convient le mieux à votre audience. Si vous optez pour plusieurs étapes, prenez soin de rappeler à l’internaute le nombre d’étapes auquel il doit s’attendre à l’aide d’une barre de progression et limitez à 3 le nombre d’étapes.
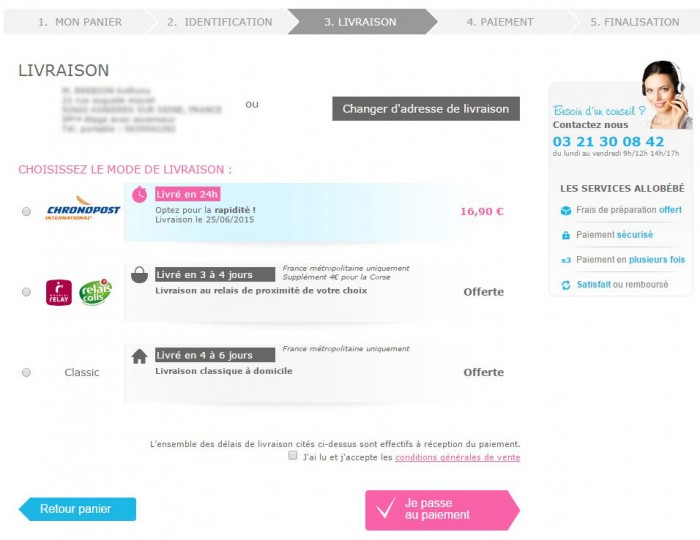 Vous pouvez aussi mettre en place un système de commande rapide à l’image d’Amazon pour vos clients ayant déjà enregistré leur moyen de paiement, ce qui leur permet de gagner encore plus de temps.
Vous pouvez aussi mettre en place un système de commande rapide à l’image d’Amazon pour vos clients ayant déjà enregistré leur moyen de paiement, ce qui leur permet de gagner encore plus de temps.
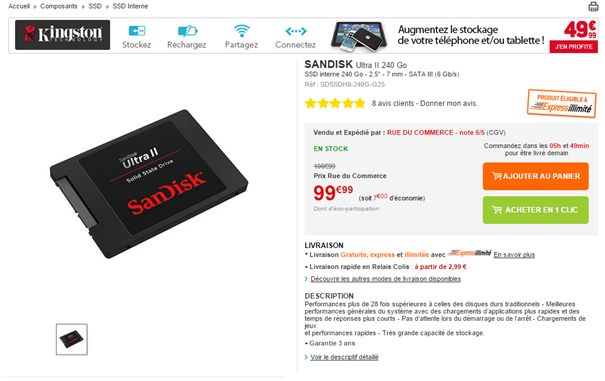
5. Limitez les distractions à chaque étape de votre tunnel de commande
Les distractions sont tous les éléments qui détournent l’internaute de l’action initiale qu’on attend de lui. Il s’agit d’éléments visuels, de messages, d’offres ou plus simplement d’éléments d’interfaces qui réclament un effort mental de sa part pour distinguer le message principal de tout ce qui se révèle être du bruit. L’attention qu’il porte à décrypter ces éléments est autant d’énergie perdue à analyser le message clé. Dans certains cas extrêmes, mais assez fréquents, ces distractions peuvent littéralement l’inciter à quitter la page pour aller consulter d’autres offres, comme dans l’exemple ci-dessous, où le bouton d’action pour entamer le processus de commande est noyé au milieu d’offres promotionnelles.
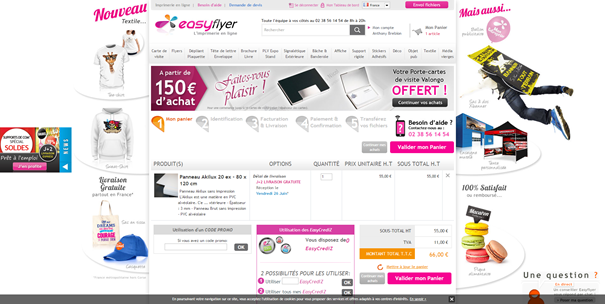
Pour limiter ces distractions, de nombreux sites vont jusqu’à supprimer les éléments de navigation habituels, réduisant ainsi les possibilités d’action de l’internaute au strict minimum, à savoir passer à l’étape suivante.

6. Multipliez les moyens de paiement
Proposez-vous les bons moyens de paiement pour vos différentes audiences ? Si vous avez une part importante de prospects venant de l’étranger, certains modes de paiement seront peut-être nécessaires (ex : American Express pour les Américains, achat sur facture ou prélèvement bancaire en Allemagne…). Analysez la provenance géographique de vos internautes et renseignez-vous sur les modes de paiement privilégiés dans chaque pays.
D’autres moyens de paiement universels et rapides, comme PayPal, peuvent aussi intéressés les internautes réfractaires à donner leur numéro de carte de crédit à des sites e-commerces peu connus ou manquant de légitimité. Certains internautes n’aiment tout simplement pas entrer de longs numéros de carte bancaire, qui plus est sur téléphone mobile, ou n’ont tout simplement pas leur carte à portée de main. Facilitez-leur la tâche.
N’oubliez pas non plus d’afficher la liste des moyens de paiement accepté pour rassurer vos internautes avant même qu’ils n’arrivent à l’étape de paiement.
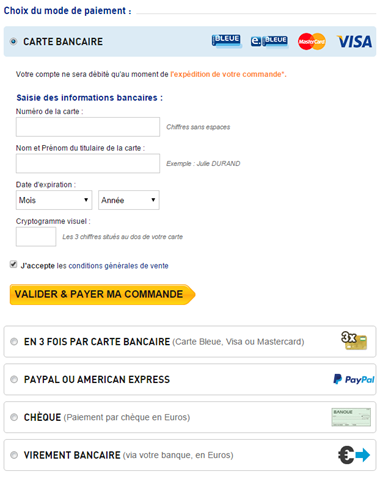
 Au moment du paiement, il n’est pas non plus inutile de leur rappeler toutes les options à disposition, comme le fait LDLC.com.
Au moment du paiement, il n’est pas non plus inutile de leur rappeler toutes les options à disposition, comme le fait LDLC.com.
7. Rassurez vos internautes
Tous les sites e-commerce ne bénéficient pas de la crédibilité et de la notoriété d’Amazon, Cdiscount ou Vente Privée. Si vous êtes un e-commerçant peu connu, vous ne devez pas négliger la confiance que vous inspirez à vos internautes.
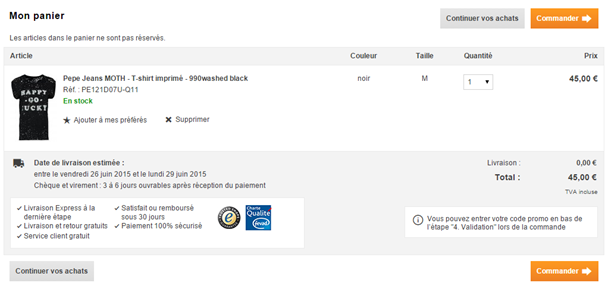
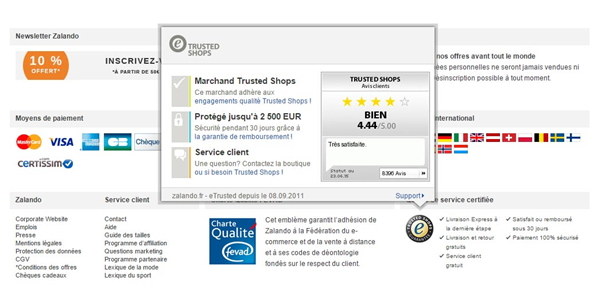
De nombreux éléments entrent en ligne de compte, mais vous pouvez déjà rassurer vos internautes en indiquant clairement sur votre site les différents moyens de vous contacter : numéros de téléphone et adresses email de contact (commercial, facturation, support…), adresse physique, etc. Si vous bénéficiez de tiers de confiance, n’hésitez pas à afficher ces labels ou sceaux sur les pages de votre tunnel de commande, en commençant par votre page panier.
Tous les éléments de nature à rassurer vos internautes doivent figurer sur cette page, à l’image de Zalendo qui commence par rappeler à ses internautes les points clés de son offre : livraison et retour gratuit, satisfait ou remboursé sous 30 jours, etc. Notez également l’ajout de la date de livraison estimée pour répondre à une interrogation légitime des internautes ainsi que des badges de réassurance (respect de la charte Fevad, Trusted Shops).
8. Soignez vos call-to-action
Une fois sur la page panier, l’internaute identifie-t-il en quelques dixièmes de seconde, l’action qui est attendue de sa part ? Travaillez la position de votre bouton « Commander » ou « Poursuivre » et assurez-vous qu’il soit visible au-dessus de la ligne de flottaison, sans avoir à scroller. Au besoin, répéter le bouton, avant et après le tableau récapitulatif des produits mis au panier.
La visibilité du bouton tient également à son contraste. Le code couleur utilisé sur votre site met-il suffisamment en avant ce bouton et se distingue-t-il des autres éléments d’interface présents sur la page ? Si vous avez d’autres boutons cliquables, établissez-vous une hiérarchie visuelle permettant d’identifier rapidement le bouton principal ?
Dans l’exemple ci-dessous, le style appliqué à chaque lien ne fait en rien ressortir le bouton permettant de passer à l’étape suivante et les options d’up-selling sont trop mises en avant, de même que la possibilité d’entre un code de réduction.
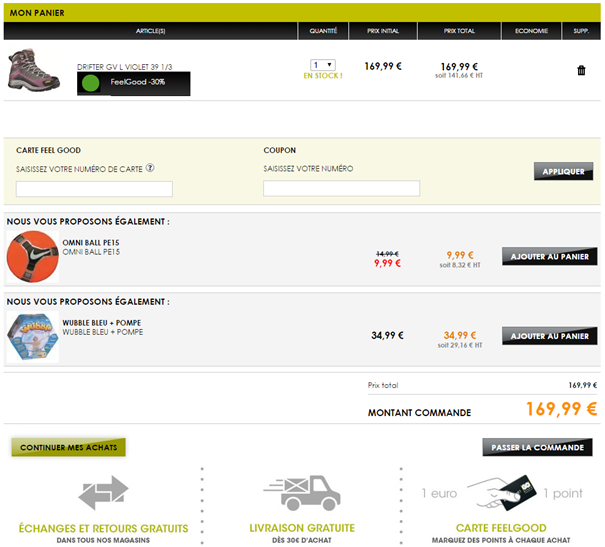
9. Repensez les fonctionnalités autour du panier d’achat
Lorsque nous avons abordé les principales raisons de l’abandon de panier, nous avons évoqué le fait que les internautes considéraient parfois le panier d’achat comme un outil pour mettre de côté les produits intéressants et les comparer ultérieurement. Très clairement, ils en détournent l’utilisation, ce qui peut fausser vos analyses si vous vous basez sur le taux d’abandon de panier pour optimiser votre tunnel de conversion. Ce comportement ne traduit en effet ni un désintérêt pour vos produits ni des problèmes d’ergonomie de votre tunnel de commande. Mieux vaut donc tenter d’isoler ce type de comportement en proposant des fonctionnalités qui y répondront. L’analyse de votre taux d’abandon n’en sera que plus juste.
De nombreux sites ont déjà intégré cet aspect en proposant des fonctionnalités de mises en favoris ou de création de liste d’achat. Le tracking et l’analyse de l’utilisation de ces fonctionnalités peuvent vous apporter beaucoup d’information sur l’intention de l’internaute et l’état d’avancement de sa décision d’achat. Est-il là pour acheter ou juste se renseigner ?
La réponse vous apportera un éclairage intéressant sur votre taux d’abandon de panier et sur la démarche à suivre pour réactiver les internautes n’étant pas allés jusqu’à la transaction. Nous aborderons justement ce point spécifique dans le 4ème et dernier billet de cette série.
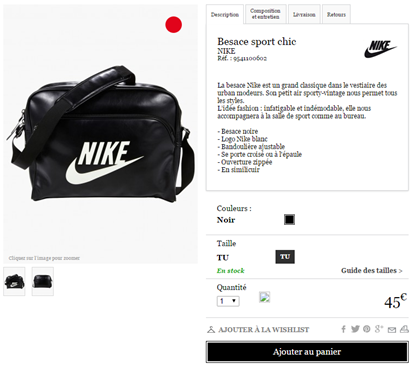
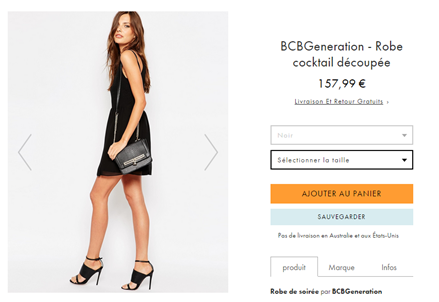
10. Pensez au remarketing sur site !
Par remarketing sur site, nous incluons tous les outils permettant d’identifier en temps réel le moment où l’internaute perd en engagement, est sur le point d’abandonner son panier ou de quitter le site. Une fois cette intention détectée, vous le réengagez avec un message personnalisé compte tenu de son historique de navigation et du contenu de son panier. Il peut s’agir de lui proposer une incentive pour l’inciter à convertir (ex. : frais de livraison offerts si le montant de son panier dépasse un certain seuil, coupon de réduction, etc.) ou simplement récupérer son adresse email pour le réengager ultérieurement via d’autres canaux. Des solutions comme AB Tasty vous aident à mettre en place de tels scénarios de réactivation personnalisés et en temps réel, de manière très simple, sans avoir à intervenir sur le code de vos pages web et à faire appel à votre équipe technique.
Autres techniques pour réactiver les internautes ayant abandonné leur panier
Les internautes n’achètent pas d’emblée lors de leur première visite. Si 70% abandonnent leur panier, c’est en grande partie parce qu’ils ne sont pas prêts à acheter et doivent encore murir leur réflexion. Cela veut-il qu’il faille se désintéresser de ces internautes et ne rien faire ? Non, plusieurs techniques peuvent être activées après que l’abandon de panier ait eu lieu pour réengager les internautes. On en retiendra principalement 2 : le retargeting publicitaire et les programmes de réactivation par email.
Retargeting publicitaire
Le retargeting publicitaire consiste à garder trace des internautes qui visitent votre site et mettent un produit au panier puis à leur diffuser une publicité alors qu’ils consultent d’autres sites. L’objectif est multiple : augmenter la présence à l’esprit de votre marque pour l’internaute qui n’est plus en phase de recherche, s’associer à des supports publicitaires parfois haut de gamme qui peuvent améliorer votre crédibilité si votre marque est peu connue ou encore pousser une incentive sur le contenu du panier abandonné pour inciter à la revisite et à la conversion. Vous avez effectivement toute latitude pour cibler les internautes (ex. : uniquement ceux ayant mis un certain montant dans leur panier ou une certaine catégorie de produit) et adapter la création publicitaire en jouant sur la personnalisation des messages (ex. : réutiliser le visuel du produit qui avait été mis au panier, etc.).
Plusieurs solutions de retargeting existent sur le marché français : Criteo, Next Performance, AdRoll, Google, etc. Elles fonctionnent globalement toutes de la même manière : quand vous allez sur un site e-commerce, le prestataire de remarketing pose un cookie sur votre ordinateur avec les produits vus et/ou mis au panier (ex. : des chaussures de sport Nike bleues). Quand vous allez sur un site web partenaire publicitaire de ce prestataire, le serveur du site lit le cookie, se rend compte que vous êtes passé sur le site e-commerce et affiche une publicité pour des chaussures de sport Nike bleues.
Quelle est l’efficacité du retargeting publicitaire sur l’abandon de panier ? En moyenne, le taux de clic d’une campagne display classique varie entre 0.05% et 0.1% alors que pour le retargeting, le taux de clics peut doubler et atteindre 0.2%. Si on s’intéresse au taux de conversion, on constate des taux pouvant aller jusqu’à 20% pour le trafic retargeté alors que la moyenne s’établit à 2% pour le trafic classique.
Programmes de réactivation par email
Une autre solution pour inciter les internautes à revenir sur le site finaliser leur achat consiste à leur envoyer un email de type transactionnel. L’objectif est de leur envoyer des relances par email échelonnées dans le temps. Lors de la 1ère relance, vous leur rappellerez par exemple le contenu de leur panier, puis vous pourrez leur proposer une offre promotionnelle ou un code de réduction dans un 2ème temps pour les inciter à convertir. De la qualité de votre scénario de relance dépendra l’efficacité de votre programme de réactivation. Deux critères sont notamment à prendre en compte : le timing d’envoi et le contenu de l’email.
Le délai idéal pour le 1er envoi semble être de moins de 24 h après la visite. Une étude d’Hybris a notamment démontré que 72% des internautes ayant abandonné leur panier et étant revenu naturellement finalisé leur transaction naturellement l’ont fait dans les 24 h suivant leur mise au panier. Mais l’étude montre également qu’il peut s’écouler 2 semaines pour que 95% de ces internautes finalisent leur transaction. Un seul email n’est donc pas suffisant. Le nombre et la fréquence de vos envois dépendront bien sûr du comportement de visites de vos acheteurs.
Concernant le contenu de l’email, il est conseillé d’insérer le visuel du/des produit(s) mis au panier pour personnaliser au maximum le message. Des éléments de réassurance sur la livraison, les moyens de paiement et bien sûr un call to action pour inciter l’internaute à retourner sur le site doivent bien sûr être présents. N’oubliez pas de préciser à l’internaute que son panier a été sauvegardé et qu’il pourra le récupérer en un clic. D’ailleurs, l’URL de destination du call to action peut renvoyer vers une page panier pré-rempli. Cette option peut, en revanche, être trop intrusive si le montant du panier est élevé et contient des produits complexes demandant plus de réflexion avant achat. Il est alors plus judicieux de renvoyer l’internaute sur la page produit reprenant l’argumentaire commercial (fiche technique, présentation vidéo, avis clients, etc.). Plus vous fournirez d’information sur le produit, plus vous apporterez à l’internaute les informations nécessaires à sa prise de décision. Intégrez également d’autres éléments pour inciter l’internaute à agir rapidement : rappel de l’état des stocks, offre tarifaire limitée dans le temps, etc. Les remises sont un levier très fort, 54% des internautes déclarent en effet être prêts à acheter des produits abandonnés dans leur panier si ces derniers étaient proposés moins chers.
Quelle est l’efficacité de ces programmes de réactivation par email ? Selon SaleCycle, un fournisseur de solutions de remarketing, 46% des emails de réactivation seraient ouverts et 13% cliqués. Un tiers de ces clics amènerait effectivement à un achat. Plus globalement, un programme de réactivation par email générerait entre 4.5 et 6% de ventes additionnelles.
Bien sûr, pour qu’un programme de réactivation par email soit applicable, vous devez avoir capturé l’adresse email de l’internaute. Si l’utilisateur a déjà un compte et est identifié, cela ne pose pas de problème. Dans le cas contraire, essayez de collecter rapidement son adresse avec un tunnel en plusieurs étapes. S’il ne va pas au-delà de l’étape de spécification de ses coordonnées (prénom, nom, adresse, email…), vous aurez au moins le moyen de le relancer. Malheureusement, 85% des internautes qui abandonnent leur panier restent anonymes. Les programmes de réactivation par email sont donc difficilement « scalables » et doivent être utilisés conjointement avec le retargeting publicitaire ou une autre forme de remarketing sur site, comme évoqué dans notre précédent article.
Adaptez vos leviers au contexte !
En conclusion, il est important de dissocier les abandons de panier (les internautes n’étant pas rentrés dans le tunnel de commande) des abandons de tunnel (ex. : l’internaute s’est créé un compte, à rentrer ses coordonnées, etc.). Ces 2 comportements révèlent des différences de maturité dans le processus de décision d’achat, que vous n’adresserez pas de la même façon. Selon les cas, vous serez amenés à activer tel ou tel levier de remarketing ou à adapter vos messages selon la typologie d’abandon.







