Il s’agit du premier article d’une série destinée à vous aider à interpréter correctement les résultats de vos tests A/B. Pour ce 1er article nous nous nous intéressons à une question récurrente : combien de temps doit durer un test avant de pouvoir en tirer des conclusions ?
La question sous-jacente est en effet cruciale et peut se résumer de la façon suivante : à partir de quand peut-on arrêter un test qui semble donner des résultats ? De la réponse dépendra la pertinence de l’analyse et le gain réel du test. En effet, il n’est pas rare de voir des tests donner de bons résultats durant la phase d’expérimentation puis, une fois les modifications mises en production, ne plus constater les mêmes résultats. Dans la majorité des cas, une erreur commise durant l’expérimentation est à l’origine de cet amer constat : le test a été arrêté trop tôt et les résultats à cet instant vous induisent en erreur. Prenons un exemple pour illustrer la nature du problème.
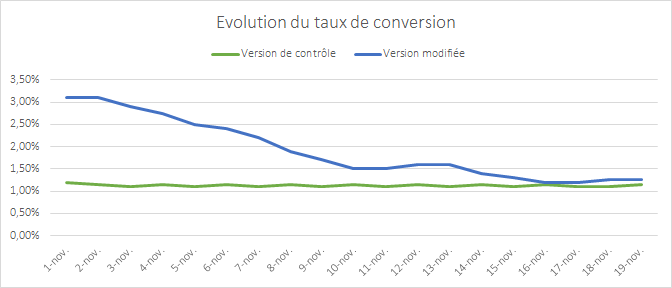
L’image précédente représente l’évolution du taux de conversion de 2 versions d’une page faisant l’objet d’un test. Dès le début du test, la 1re version semble se détacher et surperformer. L’écart entre les 2 versions se réduit progressivement au fil du temps et 2 semaines après le début du test, plus aucune différence notable n’est constatée. Ce phénomène de convergence des résultats est typique si la modification apportée n’a pas d’impact réel sur la conversion.
L’apparente surperformance au début du test s’explique simplement : il est rare que les échantillons soient représentatifs de votre audience au démarrage du test. Il faut en effet du temps pour que vos échantillons intègrent tous vos profils d’internautes et donc tous leurs comportements. Si vous arrêtez votre test trop tôt, par exemple au bout d’1 semaine dans l’exemple ci-dessus, vous allez prendre une décision erronée, car vos données sont incomplètes.
Le problème étant posé, voyons de façon pratique comment éviter de tomber dans ce piège. Il existe plusieurs critères sur lesquels vous baser pour déterminer quand vous fier aux résultats affichés par votre solution d’A/B testing.
- L’indice de confiance statistique
- La taille de l’échantillon
- La représentativité de votre échantillon
- La période du test et le device testé
1. L’indice de fiabilité statistique
Toutes les solutions d’A/B testing affichent dans leur reporting un indicateur de fiabilité statistique qui mesure la probabilité que les différences de résultats constatés entre chaque échantillon ne soient pas liées au hasard. Cet indicateur, calculé selon le test du Khi Deux, est le 1er indicateur sur lequel se baser. L’usage chez les statisticiens veut que l’on considère un test fiable à partir d’un taux de 95 %. On accepte donc de se tromper dans 5 % des cas et que les résultats des 2 versions puissent être identiques.
Se baser uniquement sur cet indicateur pour juger du moment opportun d’arrêter un test est pourtant une erreur. S’il s’agit d’une condition nécessaire pour juger de la fiabilité d’un test, elle n’est pas suffisante. Autrement dit, tant que vous n’avez pas atteint ce seuil, vous ne pouvez pas prendre de décision, et une fois ce seuil atteint, vous devez encore prendre certaines précautions.
Par ailleurs, il faut bien comprendre ce que signifie le test du Khi Deux. Celui-ci permet de rejeter ou non ce qu’on appelle l’hypothèse nulle. Appliquée à l’A/B testing, celle-ci consiste à dire que 2 versions produisent des résultats identiques (et qu’il n’y a donc pas de différences entre elles). Si la conclusion du test amène à rejeter l’hypothèse nulle, cela veut donc dire qu’il y a une différence de résultats. En revanche, le test ne présage en rien de l’ampleur de cette différence.
2. La taille de l’échantillon
Il existe de nombreux outils en ligne permettant de calculer la valeur du Khi Deux en indiquant en paramètres d’entrée les 4 éléments nécessaires à son calcul (dans le cadre d’un test avec 2 versions). Vous pouvez trouver un tel outil ici.
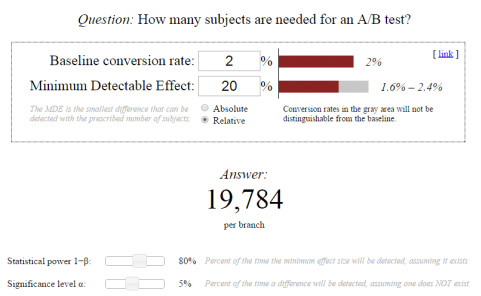
En utilisant cet outil, nous avons pris un exemple extrême pour illustrer le problème.

http://www.evanmiller.org/ab-testing/chi-squared.html
Sur cette image, le calcul du Khi Deux amène à dire que l’échantillon n° 2 converti mieux que l’échantillon n° 1 avec une fiabilité de 95 %. En revanche, les valeurs d’entrée sont extrêmement faibles et rien ne garantit que si l’on testait 1 000 personnes au lieu de 100, on conserverait le même ratio de 1 à 3 entre les taux de conversions.
C’est un peu comme jouer à pile ou face. Si la probabilité est de 50 % de tomber sur pile et 50 % sur face, il est possible, en ne jouant que 10 fois, d’avoir une distribution de 70 %/30 %. C’est uniquement en jouant un grand nombre de fois qu’on se rapproche de la distribution attendue de 50 %/50 %.
Pour pouvoir se fier au test du Khi Deux, il est donc recommandé d’avoir une taille d’échantillon conséquente. Vous pouvez calculer la taille de cet échantillon avant de démarrer votre test pour avoir une indication du moment où il est pertinent de regarder l’indicateur de fiabilité statistique. Plusieurs outils en ligne permettent de calculer cette taille d’échantillon (exemple ici). Dans la pratique cela peut s’avérer difficile, car l’un des paramètres à renseigner est le % d’amélioration attendue, ce qui n’est pas facile à évaluer, mais peut être un bon exercice pour juger de la pertinence des modifications envisagées. PS : plus le pourcentage d’amélioration attendu est faible, plus la taille de l’échantillon devra être importante pour pouvoir détecter une réelle différence. Si vos modifications ont un impact très faible, beaucoup de visiteurs devront être testés. Cela milite donc pour que vous apportiez des modifications radicales ou disruptives qui auront probablement plus d’impact sur la conversion.
3. La représentativité de votre échantillon
Si vous avez beaucoup de trafic, atteindre une taille d’échantillon suffisante n’est pas un problème et vous pouvez obtenir un taux de fiabilité statistique en seulement quelques jours, 2 ou 3 parfois. Pour autant, arrêter un test dès lors que les conditions de taille d’échantillons et de fiabilité statistique sont satisfaites n’est pas la garantie de reproduire les résultats en situation réelle.
Le point clé, souvent sous-estimé, consiste à tester aussi longtemps qu’il le faut pour inclure dans votre échantillon tous vos segments d’audience. En effet, les tests statistiques partent du postulat que vos échantillons sont distribués de façon identique, autrement dit que la probabilité de convertir est la même pour tous les internautes. Or, ce n’est pas le cas : cette probabilité varie en fonction de différents facteurs tels que le temps, l’emplacement géographique ou encore les préférences utilisateurs.
2 facteurs sont notamment très importants à prendre en compte.
- Vos cycles commerciaux. Les internautes n’achètent pas directement une fois qu’ils découvrent votre site. Ils s’informent, comparent, murissent leur réflexion… Entre le moment où ils sont soumis à l’un de vos tests et le moment où ils convertissent, il peut s’écouler 1, 2, voire 3 semaines. Si votre cycle d’achat est de 3 semaines et que vous ne testez que sur 1 semaine, votre échantillon ne sera pas représentatif, car notre outil enregistrera les visites de tous les internautes, mais n’enregistrera pas les conversions d’une partie d’entre eux pour lesquels votre test aura pourtant un impact. Nous vous conseillons donc de tester sur au moins 1 cycle commercial complet, 2 idéalement.
- Vos sources de trafic. Votre échantillon doit inclure l’ensemble de vos sources de trafic (emailing, liens sponsorisés, réseaux sociaux…) et vous devez vous assurer qu’aucune de ces sources ne soit surreprésentée dans votre échantillon. Prenons un cas concret : si le canal emailing est une source faible de trafic, mais importante de revenus, et que vous menez un test pendant une campagne emailing, vous allez inclure dans votre échantillon des internautes qui ont une plus forte propension à acheter. Celui-ci ne sera plus aussi représentatif. Il est également primordial d’avoir connaissance des opérations d’acquisition d’envergure et si possible ne pas tester sur ces périodes. Il en va de même pour les tests durant les soldes ou tous autres temps forts promotionnels qui attirent des internautes au comportement atypique. En réitérant les mêmes tests en dehors de ces périodes, vous constaterez souvent des différences de résultats moins marquées.
S’assurer de la représentativité de votre échantillon s’avère au final assez difficile, car vous maîtrisez peu la nature des internautes qui participent à votre test. Vous pouvez pallier ce problème de 2 manières. La première est de prolonger votre test plus que nécessaire pour vous rapprocher d’une distribution normale de vos internautes. La deuxième consiste à cibler vos tests pour n’inclure dans votre échantillon qu’une population spécifique. Ex : vous pouvez exclure de vos tests tous les internautes qui viennent de vos campagnes d’emailing si vous savez qu’ils biaisent vos résultats. Vous pouvez aussi cibler uniquement les nouveaux visiteurs pour ne pas inclure d’internautes bien avancés dans leur processus d’achat et qui convertiraient, quelle que soit la version à laquelle ils sont soumis.
4. Autres éléments à prendre en compte
D’autres éléments sont à prendre en compte pour s’assurer que les conditions de votre expérimentation soient les plus proches de la réalité : le timing et le device.
- Les taux de conversion pouvant varier fortement entre les jours de la semaine, voire les heures de la journée, il est conseillé de tester sur des périodes complètes. Autrement dit, si vous lancez un test le lundi matin, il doit s’arrêter un dimanche au soir pour qu’une distribution normale des conversions soit respectée.
- De même, les taux de conversion entre mobile, tablette et desktop variant fortement, nous recommandons de tester vos sites ou pages spécifiquement pour chaque device, en utilisant les fonctionnalités de ciblage pour inclure/exclure les devices pour lesquels vos utilisateurs présentent des comportements de navigation et d’achat très différents.
Ces éléments sont à prendre en compte pour ne pas arrêter vos tests trop tôt et vous fourvoyer dans une analyse erronée des résultats. Ils expliquent également pourquoi certains tests A/A, menés sur une période trop courte ou durant une période d’activité anormale, peuvent présenter des différences de résultats ainsi qu’une fiabilité statistique, alors que vous n’avez apporté aucune modification.







