The A/B testing method involves a simple process: create two variations, expose them to your customer, collect data, and analyze the results with a statistical formula.
But, how long should you wait before collecting data? With 14 days being standard practice, let’s find out why as well as any exceptions to this rule.
Why 14 days?
To answer this question we need to understand what we are fundamentally doing. We are collecting current data within a short window, in order to forecast what could happen in the future during a more extended period. To simplify this article, we will only focus on explaining the rules that relate to this principle. Other rules do exist, which mostly correlate to the number of visitors, but this can be addressed in a future article.
The forecasting strategy relies on the collected data containing samples of all event types that may be encountered in the future. This is impossible to fulfill in practice, as periods like Christmas or Black Friday are exceptional events relative to the rest of the year. So let’s focus on the most common period and set aside these special events that merit their own testing strategies.
If the future we are considering relates to “normal” times, our constraint is to sample each day of the week uniformly, since people do not behave the same on different days. Simply look at how your mood and needs shift between weekdays and weekends. This is why a data sampling period must include entire weeks, to account for fluctuations between the days of the week. Likewise, if you sample eight days for example, one day of the week will have a doubled impact, which doesn’t realistically represent the future either.
This partially explains the two-week sampling rule, but why not a longer or shorter period? Since one week covers all the days of the week, why isn’t it enough? To understand, let’s dig a little deeper into the nature of conversion data, which has two dimensions: visits and conversions.
- Visits: as soon as an experiment is live, every new visitor increments the number of visits.
- Conversions: as soon as an experiment is live, every new conversion increments the number of conversions.
It sounds pretty straightforward, but there is a twist: statistical formulas work with the concept of success and failure. The definition is quite easy at first:
- Success: the number of visitors that did convert.
- Failures: the number of visitors that didn’t convert.
At any given time a visitor may be counted as a failure, but this could change a few days later if they convert, or the visit may remain a failure if the conversion didn’t occur.
So consider these two opposing scenarios:
- A visitor begins his buying journey before the experiment starts. During the first days of the experiment he comes back and converts. This would be counted as a “success”, but in fact he may not have had time to be impacted by the variation because the buying decision was made before he saw it. The problem is that we are potentially counting a false success: a conversion that could have happened without the variation.
- A visitor begins his buying journey during the experiment, so he sees the variation from the beginning, but doesn’t make a final decision before the end of the experiment – finally converting after it finishes. We missed this conversion from a visitor who saw the variation and was potentially influenced by it.
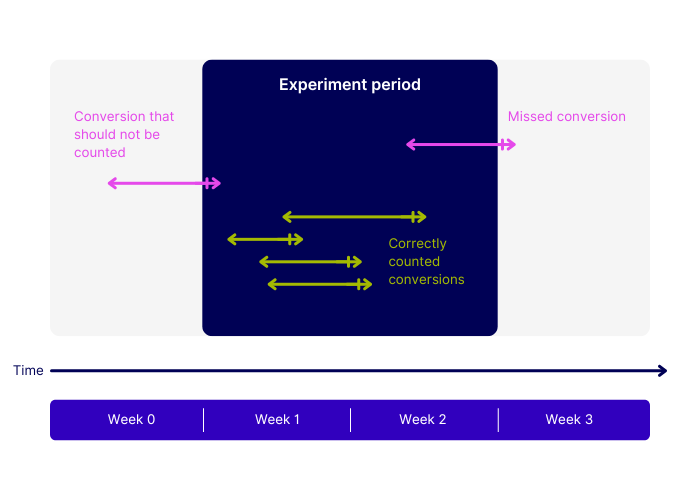
These two scenarios may cancel each other out since they have opposite results, but that is only true if the sample period exceeds the usual buying journey time. Consider a naturally long conversion journey, like buying a house, measured within a very short experiment period of one week. Clearly, no visitors beginning the buying journey during the experiment period would have time to convert. The conversion rates of these visitors would be artificially in the realm of zero – no proper measurements could be done in this context. In fact, the only conversions you would see are the ones from visitors that began their journey before the variation even existed. Therefore, the experiment would not be measuring the impact of the variation.
The delay between the effective variation and the conversion expedites the conversion rate. In order to mitigate this problem, the experiment period has to be twice as long as the standard conversion journey. Doing so ensures that visitors entering the experiment during the first half will have time to convert. You can expect that people who began their journey before the experiment and people entering during the second half of the experiment period will cancel each other out: The first group will contain conversions that should not be counted, and some of the second group’s conversions will be missing. However, a majority of genuine conversions will be counted.
That’s why a typical buying journey of one week results in a two-week experiment, offering the right balance in terms of speed and accuracy of the measurements.
Exceptions to this rule
A 14-day experiment period doesn’t apply to all cases. If the delay between the exposed variation and the conversion is 1.5 weeks for instance, then your experiment period should be three weeks, in order to cover the usual conversion delay twice.
On the other hand, if you know that the delay is close to zero, such as in the case of a media website, where you are trying to optimize the placement of an advertisement frame on a page where visitors only stay a few minutes, you may think that one day would be enough based on the this logic, but it’s not.
The reason being that you would not sample every day of the week, and we know from experience that people do not behave the same way throughout the week. So even in a zero-delay context, you still need to conduct the experiment for an entire week.
Takeaways:
- Your test period should mirror the conditions of your expected implementation period.
- Sample each day of the week in the same way.
- Wait an integer number of weeks before closing an A/B test.
Respecting these rules will ensure that you’ll have clean measures. The accuracy of the measure is defined by another parameter of the experiment: the total number of visitors. We’ll address this topic in another article – stay tuned.







