Statistical hypothesis testing implies that no test is ever 100% certain: that’s because we rely on probabilities to experiment.
When online marketers and scientists run hypothesis tests, they’re both looking for statistically relevant results. This means that the results of their tests have to be true within a range of probabilities (typically 95%).
Even though hypothesis tests are meant to be reliable, there are two types of errors that can still occur.
These errors are known as type 1 and type 2 errors (or type i and type ii errors).
Let’s dive in and understand what type 1 and type 2 errors are and the difference between the two.
Understanding Type I Errors
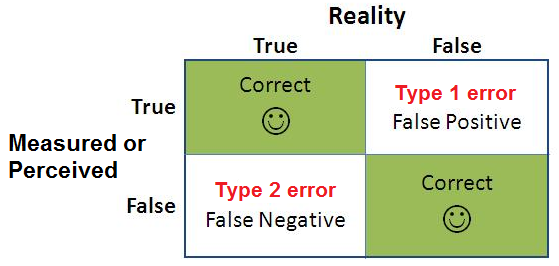
Type 1 errors – often assimilated with false positives – happen in hypothesis testing when the null hypothesis is true but rejected. The null hypothesis is a general statement or default position that there is no relationship between two measured phenomena.
Simply put, type 1 errors are “false positives” – they happen when the tester validates a statistically significant difference even though there isn’t one.
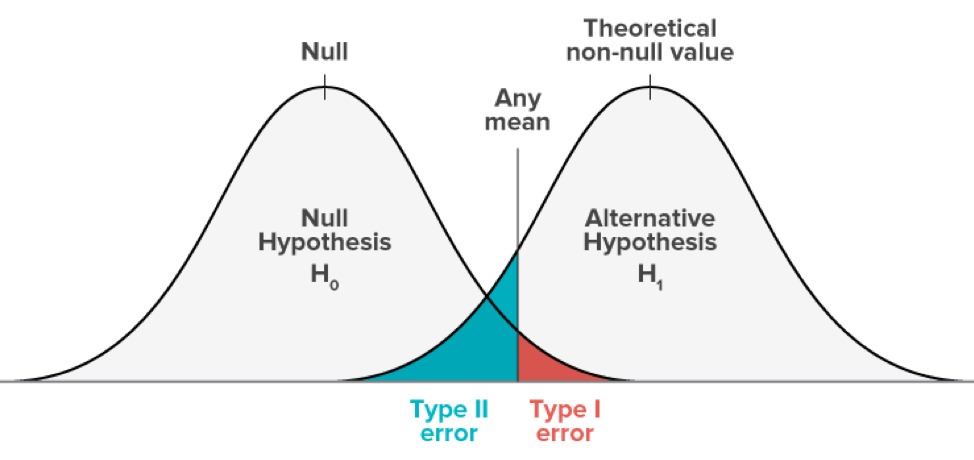
Type 1 errors have a probability of “α” correlated to the level of confidence that you set. A test with a 95% confidence level means that there is a 5% chance of getting a type 1 error.
Consequences of a Type 1 Error
Why do type 1 errors occur? Type 1 errors can happen due to bad luck (the 5% chance has played against you) or because you didn’t respect the test duration and sample size initially set for your experiment.
Consequently, a type 1 error will bring in a false positive. This means that you will wrongfully assume that your hypothesis testing has worked even though it hasn’t.
In real-life situations, this could potentially mean losing possible sales due to a faulty assumption caused by the test.
Related: Sample Size Calculator for A/B Testing
A Real-Life Example of a Type 1 Error
Let’s say that you want to increase conversions on a banner displayed on your website. For that to work out, you’ve planned on adding an image to see if it increases conversions or not.
You start your A/B test by running a control version (A) against your variation (B) that contains the image. After 5 days, variation (B) outperforms the control version by a staggering 25% increase in conversions with an 85% level of confidence.
You stop the test and implement the image in your banner. However, after a month, you noticed that your month-to-month conversions have actually decreased.
That’s because you’ve encountered a type 1 error: your variation didn’t actually beat your control version in the long run.
Related: Frequentist vs Bayesian Methods in A/B Testing
Want to avoid these types of errors during your digital experiments?
AB Tasty is an a/b testing tool embedded with AI and automation that allows you to quickly set up experiments, track insights via our dashboard, and determine which route will increase your revenue.
Understanding Type II Errors
In the same way that type 1 errors are commonly referred to as “false positives”, type 2 errors are referred to as “false negatives”.
Type 2 errors happen when you inaccurately assume that no winner has been declared between a control version and a variation although there actually is a winner.
In more statistically accurate terms, type 2 errors happen when the null hypothesis is false and you subsequently fail to reject it.
If the probability of making a type 1 error is determined by “α”, the probability of a type 2 error is “β”. Beta depends on the power of the test (i.e the probability of not committing a type 2 error, which is equal to 1-β).
There are 3 parameters that can affect the power of a test:
- Your sample size (n)
- The significance level of your test (α)
- The “true” value of your tested parameter (read more here)
Consequences of a Type 2 Error
Similarly to type 1 errors, type 2 errors can lead to false assumptions and poor decision-making that can result in lost sales or decreased profits.
Moreover, getting a false negative (without realizing it) can discredit your conversion optimization efforts even though you could have proven your hypothesis. This can be a discouraging turn of events that could happen to any CRO expert and/or digital marketer.
A Real-Life Example of a Type 2 Error
Let’s say that you run an e-commerce store that sells cosmetic products for consumers. In an attempt to increase conversions, you have the idea to implement social proof messaging on your product pages, like NYX Professional Makeup.
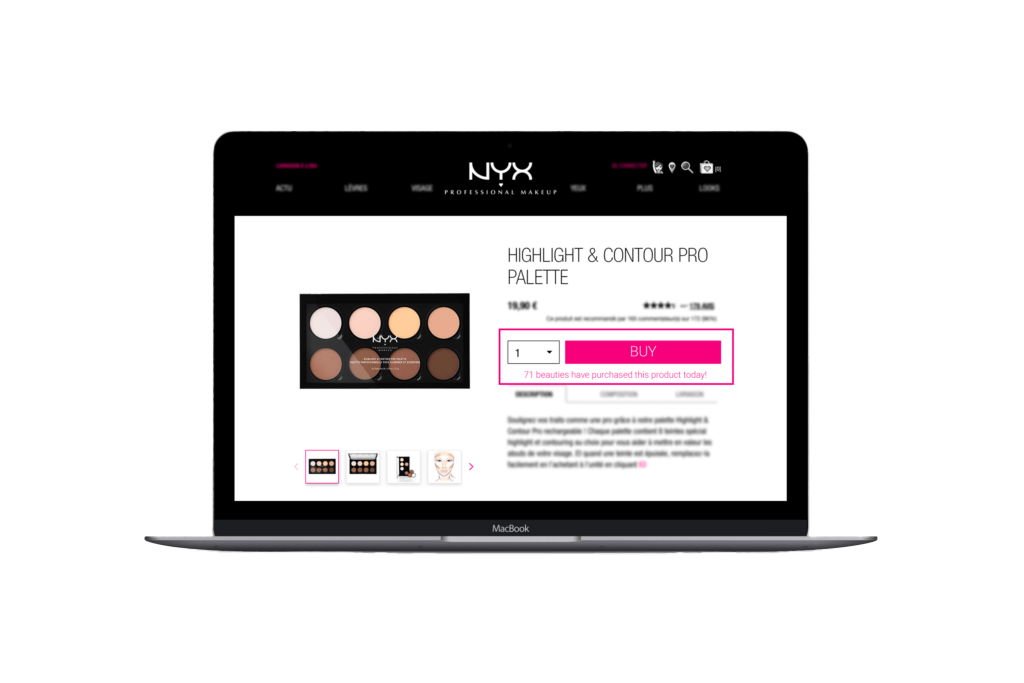You launch an A/B test to see if the variation (B) could outperform your control version (A).
After a week, you do not notice any difference in conversions: both versions seem to convert at the same rate and you start questioning your assumption. Three days later, you stop the test and keep your product page as it is.
At this point, you assume that adding social proof messaging to your store didn’t have any effect on conversions.
Two weeks later, you hear that a competitor had added social proof messages at the same time and observed tangible gains in conversions. You decide to re-run the test for a month in order to get more statistically relevant results based on an increased level of confidence (say 95%).
After a month – surprise – you discover positive gains in conversions for the variation (B). Adding social proof messages under the purchase buttons on your product pages has indeed brought your company more sales than the control version.
That’s right – your first test encountered a type 2 error!
Why are Type I and Type II Errors Important?
Type one and type two errors are errors that we may encounter on a daily basis. It’s important to understand these errors and the impact that they can have on your daily life.
With type 1 errors you are making an incorrect assumption and can lose time and resources. Type 2 errors can result in a missed opportunity to change, enhance, and innovate a project.
To avoid these errors, it’s important to pay close attention to the sample size and the significance level in each experiment.
