How Long Should You Run an A/B Test?

In this article, we consider a question that comes up time after time:  how long should an A/B test run before you can draw conclusions from it?

The underlying question is in fact a crucial one and can be summed up as follows:  at what point can you end a test that appears to be yielding results? The answer depends on the relevance of the analysis and on the actual benefits of the test.  It is not all that unusual to see tests yield good results during the trial phase and then, once the modifications are introduced, those same results are no longer seen.  In most cases, a disappointing observation of this nature is down to an error having been made during the trial phase: the test was ended too soon and the results at this point were misleading.  Let’s look at an example that illustrates the nature of the problem.

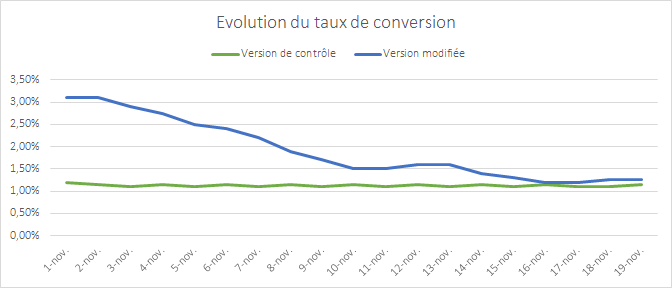
The graph above shows the change in the conversion rate of two versions of a page that were the subject of a test.  The first version appears to break away and perform extremely well.  The discrepancy between the two versions is gradually eroded as time goes by and two weeks after the test has begun there is hardly any observable difference at all.  This phenomenon in which the results converge is typical of situations in which the modification made does not have a real impact on conversion.

There is a simple explanation for the apparent outperformance at the start of the test:  it is unusual for the samples to be representative of your audience when the test starts, and you do in fact need time for your samples to incorporate all internet user profiles, and therefore all of their behaviours.  If you end the test too soon, at the end of one week in the above scenario, for example, then you will have made a bad decision as your data will be incomplete.

Now that the problem has been aired let’s have a look, practically speaking, at how you can avoid falling into this trap.  There are several criteria you should have by way of a foundation in order to determine when you can trust the results you see in your A/B testing.

• The statistical confidence level
• The size of the sample
• The representativeness of your sample
• The test period and the device being tested

1.  The statistical confidence level

All A/B testing solutions show a statistical reliability indicator that measures the probability of the difference in the results observed between each sample not being a matter of chance.  This indicator, which is calculated using the Chi-squared test, is the first indicator that should be used as a basis. It is used by statisticians to assert that a test is deemed reliable when the rate is 95% or higher.  So it is acceptable to make a mistake in 5% of cases and for the results of the two versions to be identical.

And yet it would be a mistake to use this indicator alone as a basis for assessing the appropriate time to end a test.  For the purposes of devising the conditions necessary to assess the reliability of a test, this is not sufficient.  In other words, if you have not reached this threshold then you cannot make the decision, and once this threshold has been reached then you still need to take certain precautions.

It is also important to understand what the Chi-squared test actually means.  It is a way of rejecting or not rejecting what is referred to as the null hypothesis.  This, when applied to A/B testing, is when you say that two versions produce identical results (and that there is therefore no difference between them).  If the conclusion of the test leads you to reject the null hypothesis then it means that there is a difference between the results.  However, the test is in no way an indication of the extent of this difference.

2. The size of the sample

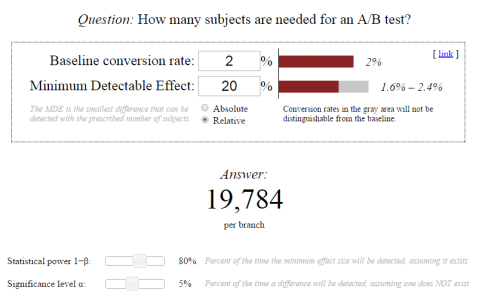
There are lots of online tools that you can use to calculate the value of Chi-squared by giving, as the input parameters, the four elements necessary to its calculation (within the confines of a test with two versions). You can use our own sample size calculator.

In using this tool, we have taken an extreme example in order to illustrate the problem.

In this diagram, the Chi-squared calculation suggests that sample 2 converts better than sample 1 with a 95% confidence level.  Having said that, the input values are very low indeed and there is no guarantee that if 1,000 people were tested rather than 100 you would still have the same 1 to 3 ratio between the conversion rates.

It’s rather like flipping a coin.  If there is a 50% probability that the coin will land heads-up or tails-up then it is possible to get a 70 % / 30 % distribution by flipping it just 10 times.  It is only when you flip the coin a very large number of times that you get close to the expected ratio of 50 % / 50 %.

So in order to have faith in the Chi-squared test, you are advised to use a significant sample size.  You can calculate the size of this sample before beginning the test to get an indication of the point at which it would be appropriate to look at the statistical reliability indicator.  There are several tools online that you could use to calculate this sample size (example here).  In practice this can turn out to be difficult, as one of the parameters to be given is the % improvement expected which is not easy to evaluate – but it can be a good exercise to assess the pertinence of the modifications being envisaged.  PS: the lower the expected improvement rate, the greater the sample size needed to be able to detect a real difference.  If your modifications have a very low impact then a lot of visitors will need to be tested.  This serves as an argument in favour of introducing radical or disruptive modifications that would probably have a greater impact on the conversion.

3. The representativeness of your sample

If you have a lot of traffic, then getting a sufficiently large sample size is not a problem and you will be able to get a statistical reliability rate in just a few days, sometimes just two or three.  Having said that, ending a test as soon as the sample size and statistical reliability conditions have been met is no guarantee that results in a real-life situation are being reproduced.

The key point – one that is often under-estimated – is to test for as long as you need to in order for all of your audience segments to be included. Actually, the statistical tests operate on the premise that your samples are distributed in an identical fashion – in other words that the conversion probability is the same for all internet users.  But this is not the case:  the probability varies in accordance with different factors such as the weather, the geographical location and also user preferences.

There are two very important factors, in particular, that must be taken into account.

• Your business cycles.  Internet users do not make a purchase as soon as they come across your site.  They learn more, they compare, and their thoughts take shape.  One, two or even three weeks might elapse between the time they are the subject of one of your tests and the point at which they convert.  If your purchasing cycle is three weeks long and you have only run the test for one week, then your sample will not be representative, as the tool records visits from all internet users but does not record the conversions of the proportion of them that have been impacted by your test.  You are therefore advised to test over at least one business cycle and ideally two.
• Your traffic sources.  Your sample must incorporate all of your traffic sources (including emails, sponsored links and social networks) and you need to make sure that no single source is over-represented in your sample.  Let’s take a concrete situation:  if the email channel is a weak source of traffic but significant in terms of revenue and you carry out a test during an email campaign, then you are going to include internet users who have a stronger tendency to make a purchase in your sample.  This would no longer be a representative sample.  It is also crucial to know about major acquisition projects and, if possible, not to test during these periods.  The same goes for tests during sales or other significant promotional periods that attract atypical internet users.  You will often see less marked differences in the results if you re-do the tests outside these periods.

It turns out that it is in fact quite difficult to make sure that your sample is representative, as you have little control over the kind of internet users who take part in your test.  There are two ways of overcoming this problem.  The first is to extend the duration of your test more than is necessary in order to get closer to the normal spread of your internet users.  The second is to target your tests so that you only include a specific population group in your sample.  For example, you could exclude all internet users who have come to you as a result of your email campaigns from your samples, if you know that this will distort your results.  You could also target only new visitors so that you do not include internet users who have reached an advanced stage in their purchasing process and who would convert regardless of the version they have.

4. Other elements to bear in mind

There are other elements to bear in mind in order to be confident that your trial conditions are as close as they can be to a real-life situation:  timing, and the device.

Conversion rates can vary massively on different days of the week and even at different times of the day and you are advised to run the test over complete periods.  In other words, if you launch the test on a Monday morning then it should be stopped on a Sunday evening so that a normal range of conversions is respected.

In the same way, conversion rates can vary enormously between mobiles, tablets and desktop computers and you are advised to test your sites or pages specifically for each device. Do this by using the targeting features to include or exclude the devices on which your users show very different browsing and purchasing behaviour patterns.

These elements should be taken into account so that you do not end your tests too soon and get led astray by a faulty analysis of the results.  They also explain why certain A/A tests carried out over a period of time that is too short, or during a period of unusual activity, can present differences in results and also differences in statistical reliability, even when you may not have made any modifications at all.

Learn more about statistical methods and A/B test reliability: download our ebook.