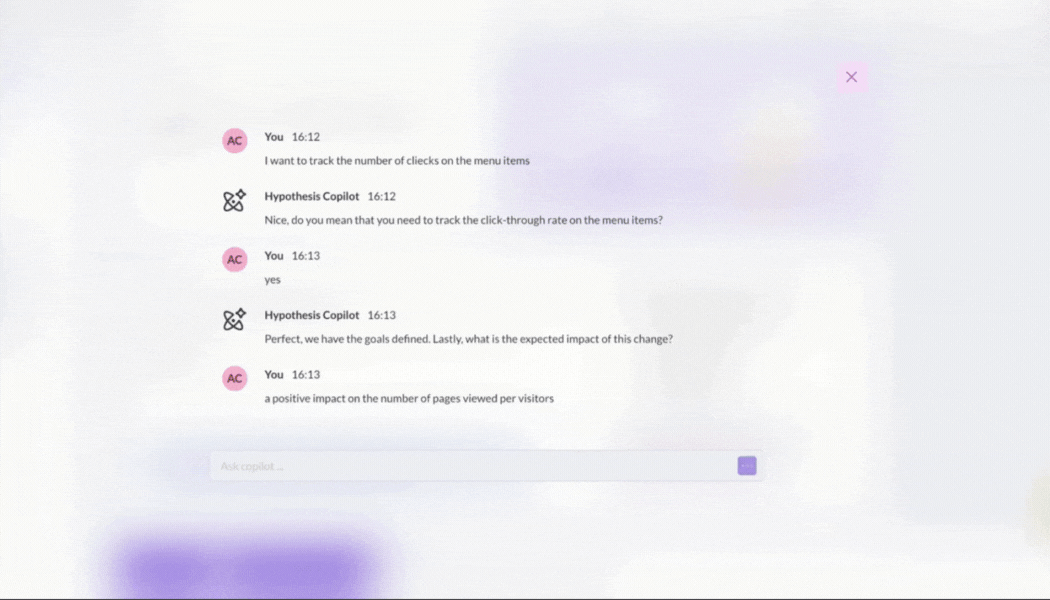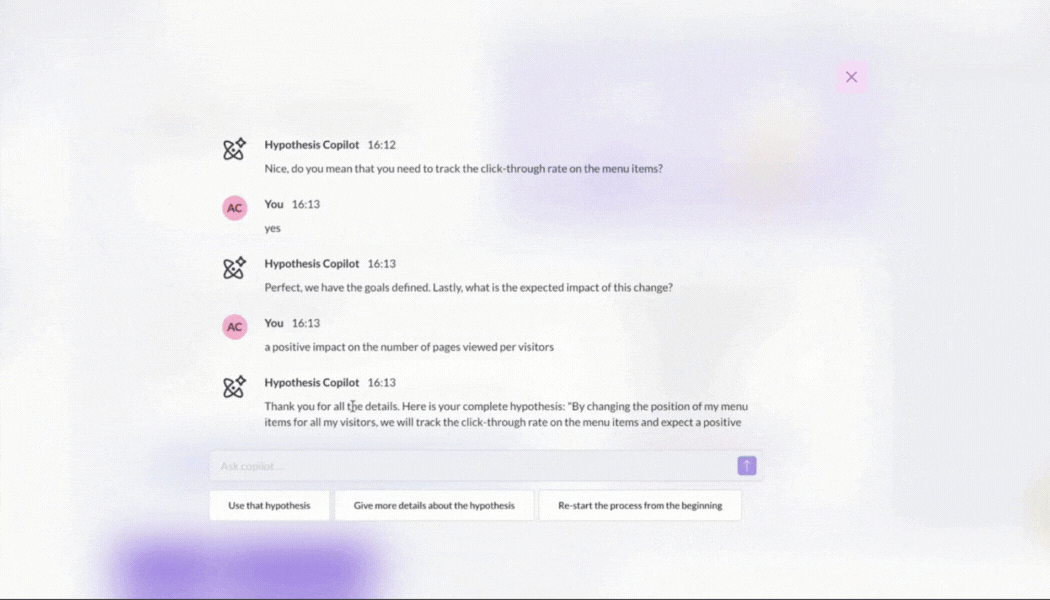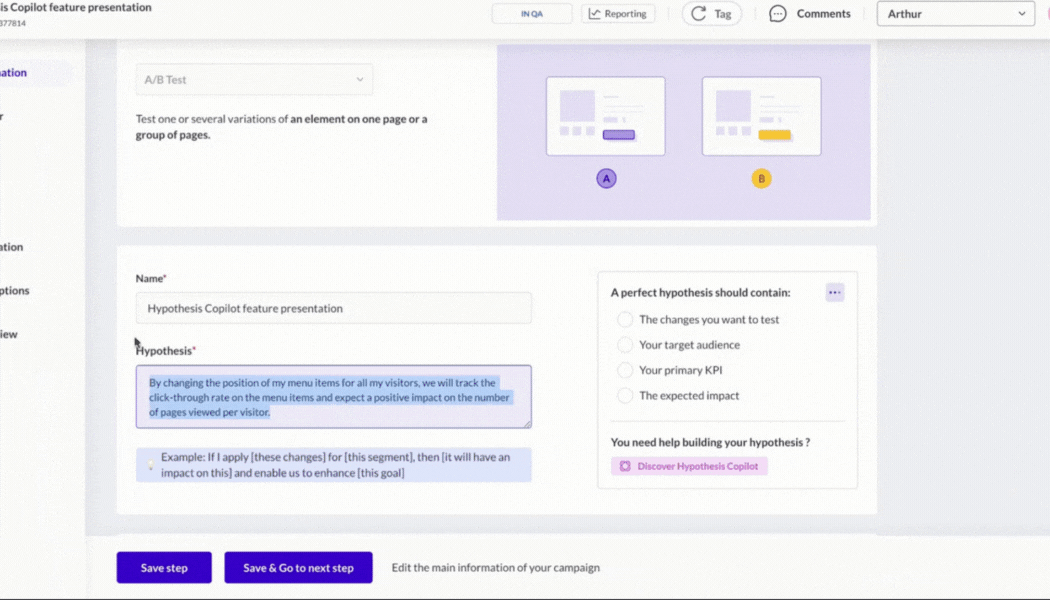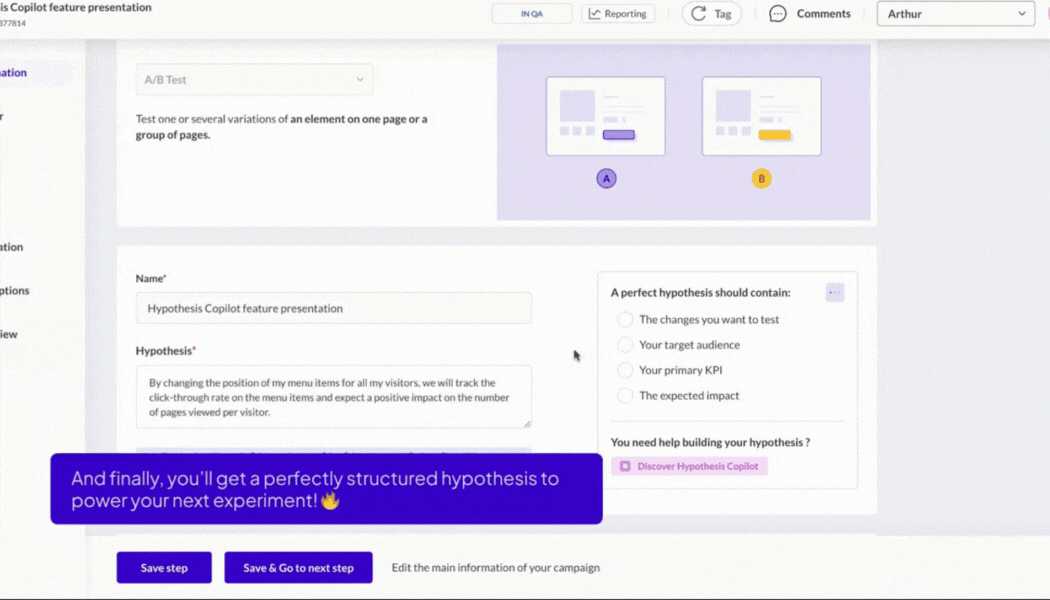
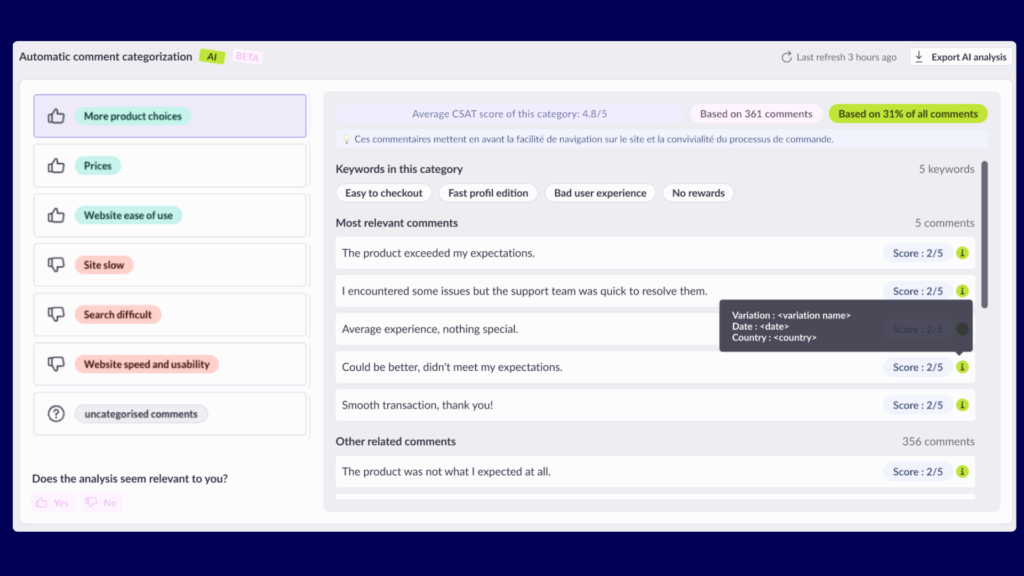
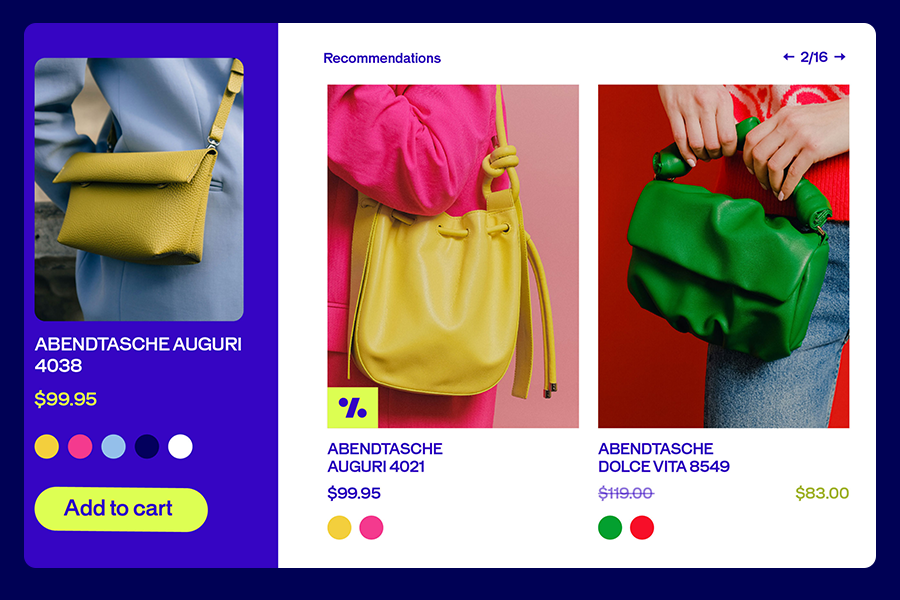
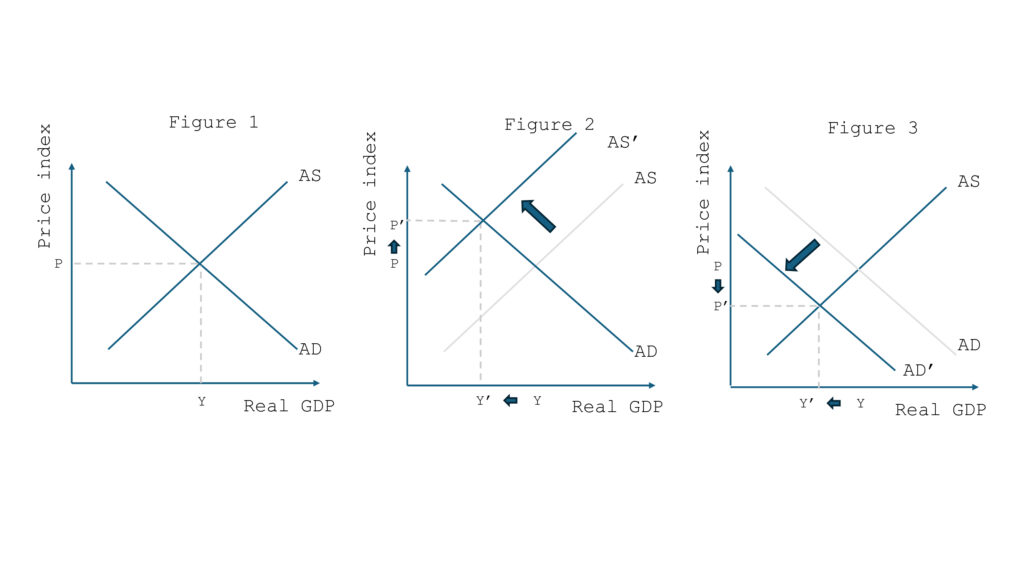
If you’ve ever run an A/B test, you know the thrill of watching those numbers tick up and down, hoping your new idea will be the next big winner. But behind every successful experiment is a secret ingredient: the statistical model that turns your data into decisions.
With so many options – Bayesian, Frequentist, CUPED, Sequential – it’s easy to feel like you’re picking a flavor at an ice cream shop you’ve never visited before. Which one is right for you? Let’s dig in!
The Scoop on Statistical Models
Statistical models are the brains behind your A/B tests. They help you figure out if your shiny new button color is actually better, or if you’re just seeing random noise. But not all models are created equal, and each has its own personality – some are straightforward, some are a little quirky, and some are best left to the pros.
Bayesian Testing Model: The Friendly Guide
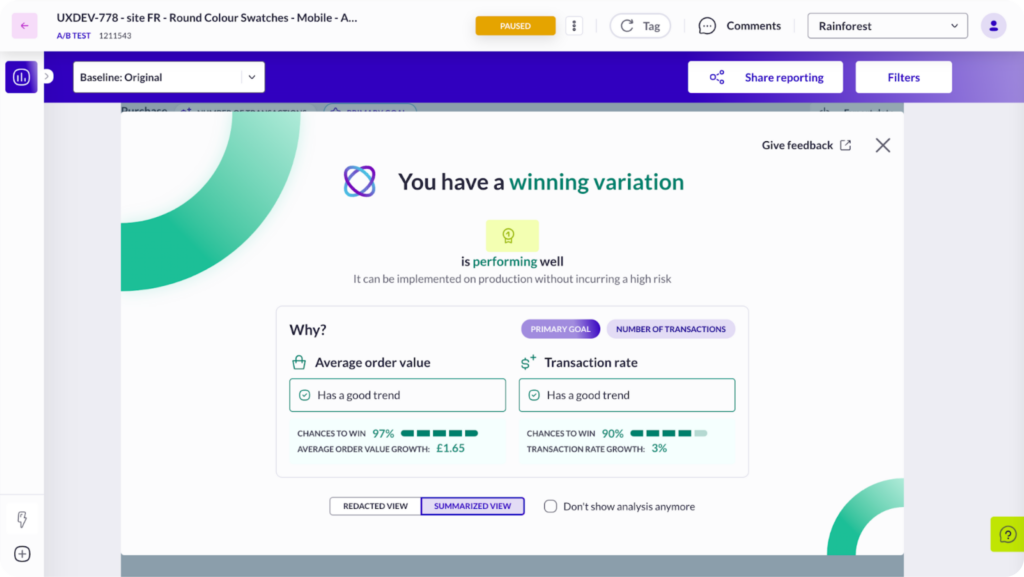
Imagine you’re asking a friend, “Do you think this new homepage is better?” The Bayesian model is that friend who gives you a straight answer: “There’s a 92% chance it is!” Bayesian statistics use probability to tell you, in plain language, how likely it is that your new idea is actually an improvement.
Bayesian analysis works by updating what you believe as new data comes in. It’s like keeping a running tally of who’s winning the race, and it’s not shy about giving you the odds. This approach is especially handy for marketers, product managers, and anyone who wants to make decisions without a PhD in statistics. It’s clear, actionable, and – dare we say – fun to use.
At AB Tasty, we love Bayesian. It’s our go-to because it helps teams make confident decisions without getting tangled up in statistical spaghetti. Most of our clients use it by default, and for good reason: it’s easy to understand, hard to misuse, and perfect for fast-paced digital teams.
Pros of Bayesian Testing:
- Results are easy to interpret (“There’s a 92.55% chance to win!”).
- Great for business decisions (and no need to decode cryptic p-values).
- Reduces the risk of making mistakes from peeking at your data.
Cons of Bayesian Testing:
- Some data scientists may prefer more traditional methods.
- Can require a bit more computing power for complex tests.
Frequentist Testing Model: The Classic Statistician
If Bayesian is your friendly guide, Frequentist is the wise professor. This is the classic approach you probably learned about in school. Frequentist models use p-values to answer questions like, “If there’s really no difference, what are the chances I’d see results like this?”
Frequentist analysis is all about statistical significance. If your p-value is below 0.05, you’ve got a winner. This method is tried and true, and it’s the backbone of academic research and many data teams.
But here’s the catch: p-values can be tricky. They don’t tell you the probability that your new idea is better; they tell you the probability of seeing your data if nothing is actually different. It’s a subtle distinction, but it trips up even seasoned pros. If you’re comfortable with statistical lingo and want to stick with tradition, the Frequentist model is a good choice. Otherwise, it can feel a bit like reading tea leaves.
Pros of Frequentist Testing:
- Familiar to statisticians and data scientists.
- Matches legacy processes in many organizations.
Cons of Frequentist Testing:
- Results can be confusing for non-experts.
- Easy to misinterpret, leading to “false positives” if you peek at results too often.
CUPED Testing Model: The Speedster (But Only for the Right Crowd)
CUPED (Controlled Experiment Using Pre-Experiment Data) is designed to go fast by using data from before your experiment even started. By comparing your test results to users’ past behavior, CUPED can reduce the noise and help you reach conclusions quicker.
But here’s the twist: CUPED only shines when your users come back again and again, like on streaming platforms (Netflix) or big SaaS products (Microsoft). If you have an e-commerce site, CUPED can actually steer you wrong, leading to misleading results.
For most e-commerce teams, CUPED is a bit like putting racing tires on a city bike, not the best fit. But if you’re running experiments on a platform with high user recurrence, it can be a powerful tool in your kit.
Pros CUPED Testing:
- Can deliver faster, more precise results for high-recurrence platforms.
- Makes the most of your existing data.
Cons of CUPED Testing:
- Not suitable for most e-commerce or low-frequency sites.
- Can lead to errors if used in the wrong context.
- More complex to set up and explain.
Sequential Testing Model: The Early Warning System
Sequential testing is your experiment’s smoke alarm. Instead of waiting for a set number of visitors, it keeps an eye on your results as they come in. If things are going south – say, your new checkout flow is tanking conversions – it can sound the alarm early, letting you stop the test and save precious traffic.
But don’t get too trigger-happy. Sequential testing is fantastic for spotting losers early, but it’s not meant for declaring winners ahead of schedule. If you use it to crown champions too soon, you risk falling for false positives – those pesky results that look great at first but don’t hold up over time.
At AB Tasty, we use sequential testing as an early warning system. It helps our clients avoid wasting time and money on underperforming ideas, but we always recommend waiting for the full story before popping the champagne.
Pros of Sequential Testing:
- Helps you spot and stop losing tests quickly.
- Saves resources by not running doomed experiments longer than necessary.
Cons of Sequential Testing:
- Not designed for picking winners early.
- Can lead to mistakes if used without proper guidance.
Which Statistic Model is Best for A/B Testing?
If you’re looking for a model that’s easy to use, hard to misuse, and perfect for making fast, confident decisions, Bayesian is your best bet – especially if you’re in e-commerce or digital marketing. It’s the model we recommend for most teams, and it’s the default for a reason.
If you have a team of data scientists who love their p-values, or you’re working in a highly regulated environment, Frequentist might be the way to go. Just be sure everyone’s on the same page about what those numbers really mean.
Running a streaming service or a platform where users log in daily? CUPED could help you speed things up – just make sure you’ve got the right data and expertise.
And if you want to keep your experiments safe from disasters, Sequential is the perfect early warning system.
Conclusion: The Right A/B Testing Model for the Right Job
Choosing a statistical model for A/B testing doesn’t have to be a headache. Think about your team, your users, and your goals. For most, Bayesian is the friendly, reliable choice that keeps things simple and actionable. But whichever model you choose, remember: the best results come from understanding your tools and using them wisely.
Ready to run smarter, safer, and more successful experiments? Pick the model that fits your needs—and don’t be afraid to ask for help if you need it. After all, even the best chefs need a good recipe now and then.
Hungry for more?
Check out our guides on Bayesian vs. Frequentist A/B Testing and When to Use CUPED. Happy testing!