Author: Hubert Wassner

Hubert has worked in the field of Data & AI since 1995, primarily regarding speech processing, then later in DNA analysis during the ‘human genome race.’ He later taught algorithmic & machine learning at ESIEA. He is currently the Chief Data Scientist at AB Tasty.

Article

Apr 1, 2026
9min read

Sample Size Calculation in A/B Testing: 7 Best Practices

Hubert Wassner

Hubert Wassner

Sample Size Calculation for A/B Tests Made Simple

At its heart, the A/B testing process is designed to generate reliable results so you can make decisions based on hard data. But working out just how many visitors you need to sample to have confidence in these can depend on a number of different factors. Fortunately, online tools can now help you take the guesswork out of the process, without the need for a math’s degree.

white calculator

How Sample Size Calculation Works

The key reason for calculating the correct sample size for a given test is to ensure that this is representative of your entire audience. This in turn will ensure that your test results are reliable and help you to avoid false positives and negatives. If your sample size is too small, you could end up with wildly misleading results. If it’s too big, you could be wasting time and resources without gaining any useful insights. 

A very general rule of thumb is to have a minimum sample of 10,000 visitors per test variation and at least 300 conversions for each. However, you can calculate the correct sample size for a given A/B test variation with the aid of a standard mathematical formula which looks like this:

Here’s a breakdown of what each letter stands for in the equation:

  • n is the required sample size per test variation
  • p1 is the Baseline Conversion Rate
  • p2 is the conversion rate lifted by absolute Minimum Detectable Effect
  • Z⍺/2 is the Z-score for Statistical Significance Level
  • Zβ is the Z-score for Statistical Power

Looks complicated? Before you start reaching for the algebra textbook, don’t panic! Instead, let’s have a look at what the above variables actually mean:

  • Baseline Conversion Rate: the current conversion rate for the specific goal that you are trying to improve. This might be something like subscription rate, transaction rate, or click though rate.
  • Minimum Detectable Effect (MDE): the smallest change in the conversion rate that you want to detect with statistical confidence. This essentially determines how sensitive your A/B test will be.
  • Statistical Significance Level: the probability that the difference in your baseline conversion rate and the conversion rate of a test variation is not caused by chance. The accepted standard for statistical significance is 95%. The Z-score for 95% significance is 1.96.
  • Statistical Power: the probability that your test will detect a real effect where one exists. Again, standard practice is to set power at 80%, meaning you have an 80% chance of catching a true winner. The Z-score for 80% power is 0.84.
Boost your conversion rates by creating personalized experiences

Fortunately, there are now a range of tools available online that will perform this somewhat intimidating calculation for you. For most of these, all you typically need to do is enter the variables above.

It’s worth noting that both the Minimum Detectable Effect (MDE) and statistical power have a direct relationship on the sample size of a test. If you want higher statistical power (i.e. more chance of catching a winner) or a smaller MDE (i.e. greater test sensitivity), your sample size will need to be bigger. That can affect the time taken for a test to run and the resources involved.

At some point, you’ll have to ask yourself: is it worth it?

Different Approaches to Calculating Sample Size

Many online platforms recommend calculating the sample size of an A/B test in the pre-test planning phase. But at AB Tasty, we think this is too late. Because If you discover that this number is too high, meaning the test would need to run too long to be practically feasible, then it is just useless to build the variant.

That’s why we’ve developed an MDE calculator specifically for the pre-test planning phase. This helps you understand the minimum uplift required and how much time you would need for an experiment to achieve statistical significance based on your actual historical data. This will ensure that you set realistic expectations before you launch a test.

Using our Minimum Detectable Effect Calculator couldn’t be easier:

1

Input

Define Your Baseline

Input your current website visitors and the conversion rate for the specific goal you intend to improve.

2

Calculate

Map the Opportunity

The calculator estimates the minimum uplift needed for significance. See exactly how many days it takes to reach your confidence threshold.

3

Launch

Eliminate Waste

Avoid wasting time and resources on tests that are unlikely to produce conclusive or statistically significant results.

We also have a Sample Size Calculator which helps you determine the required number of visitors for your test and estimate how long your test should run for to achieve the desired results. This should be used for ongoing tests, and not for pre-test planning.

To Estimate the Number of Visitors :

  • You input the current conversion rate for the goal you are trying to improve and the expected uplift between test variations.
  • Our calculator then estimates the required number of test visitors per test variation.

To Estimate the Duration of Your A/B Test:

  • In addition to the information entered in the previous step, you input the average number of daily unique visitors a tested page receives and the total number of test variations including the control version.
  • Our calculator then estimates the minimum required test duration in days to achieve the desired results. However, this number comes with a caveat, as explained below.

Best Practices and Pitfalls

Now let’s look at some of the major dos and don’ts to keep in mind when calculating test duration and sample size.

1. Run tests for a minimum of 14 days

Even if you reach your target sample size in a few days, or our test duration calculator suggests otherwise, it’s best practice to run an A/B test for a minimum of two weeks. This helps to account for variations in user behavior, such as weekday versus weekend traffic, and ensures your data is much more reliable.

2. Account for external factors like seasonality

Certain periods of the year, like Christmas, Black Friday, or Bank Holiday weekends can skew your results if you’re running a test at these times. You’ll need to take these into account if you want your sample to remain representative of your normal audience.

3. Don’t stop a test too early

You also need to avoid the temptation of checking on test results before both the test duration and sample size have been reached. Doing so dramatically increases the chances of coming to a false conclusion about the test.

Our Evi Analysis AI agent relies on statistical significance to tell you whether a particular variation is a winner. For it to do its job correctly, you should only ask Evi to interpret the results after the test has reached the number of visitors recommended by the Sample Size Calculator. That’s because Evi Analysis can’t inherently know that you planned to have a sample size of, say 100,000 visitors, but decided to stop after only 10,000.

4. Don’t overlook practical significance

Having test results that are statistically significant doesn’t automatically mean they have a practical application for your business. If it will be too costly to implement a change indicated by a test variation it might not be worth running the test in the first place.

5. Prioritize high-traffic pages

Testing should be initially focused on pages of your website that are likely to receive the most visitors. For example, the homepage, product listing pages (PLPs), or product detail pages (PDPs). The greater volume of traffic to these pages means you’ll be able to gather data more quickly and run faster tests.

6. Limit the number of variations

Testing more variations at once can seem more efficient, but it increases the risk of false positive results. If you’re testing on pages with low traffic volume, using fewer variations avoids splitting sample visitors too thinly.

7. Target broadly

When possible, run A/B tests across multiple countries or segments to increase the sample size.

Conclusion: From Guesswork to Growth

Calculating the correct sample size for your A/B tests is the key to delivering statistically significant results you can trust. But you no longer have to be a math whizz to figure out how big your sample size needs to be.

By using our MDE calculator for pre-test planning and adhering to best practices for sample size and test duration, you can ensure your A/B tests will be both more effective and more reliable.

Ready to go from calculating to converting?

FAQs

Still have questions about sample size calculators? Here are the answers you need.

Why is sample size calculation important in A/B testing?

Sample size calculation allows your test to have enough power to detect a meaningful difference between variants while avoiding wasted resources. Too small a sample may lead to false negatives, whereas too large of a sample size may be inefficient or expose too many users unnecessarily.

Which approach should I use to calculate sample size?

Usually, you use a power analysis that considers the expected effect size, significance level (α), and desired power (1−β). Tools like online calculators or statistical software can help, working under the notion a binomial or normal approximation depending on your metric.

How do you determine the minimum detectable effect (MDE) for an A/B test?

MDE is the smallest change between your control and variant that you consider practically significant. This is calculated based on business goals, baseline conversion rates, and the statistical power you want – usually by deciding what lift in metrics (e.g., click-through rate, revenue) would justify implementing the new variant.

Profile Image

About the Author

Hubert Wassner

Hubert Wassner is Chief Data Scientist at AB Tasty with over thirty years of experience in AI and machine learning. He builds advanced statistical models, shares insights on the blog, and helps brands make confident, data-driven decisions. His most recent achievement is obtaining a patent for RevenueIQ.

Share on

LinkedIn Facebook Twitter

Article

Feb 2, 2026
10min read

Frequentist vs Bayesian Methods in A/B Testing

Hubert Wassner

Hubert Wassner

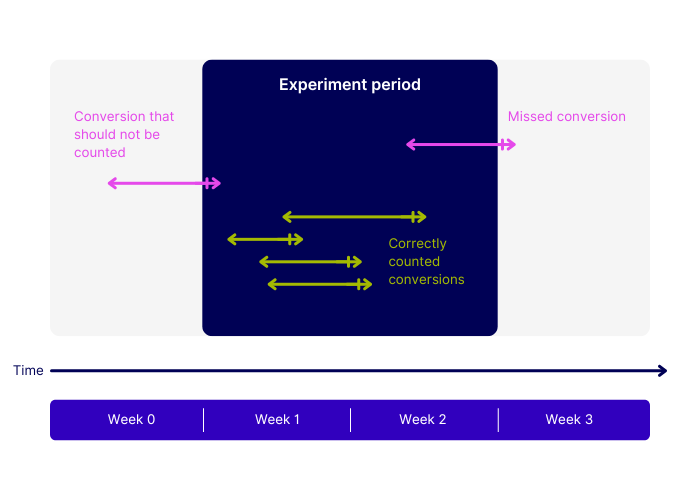
When you’re running A/B tests, you’re making a choice—whether you know it or not.

Two statistical methods power how we interpret test results: Frequentist vs Bayesian A/B testing. The debates are fierce. The stakes are real. And at AB Tasty, we’ve picked our side.

If you’re shopping for an A/B testing platform, new to experimentation, or just trying to make sense of your results, understanding these methods matters. It’s the difference between guessing and knowing. Between implementing winners and chasing false positives.

Let’s break it down.

AB testing Bayesian vs frequentist methods

What is Inferential Statistics?

Both Frequentist and Bayesian methods live under the umbrella of inferential statistics.

Unlike descriptive statistics—which simply describes what already happened—inferential statistics help you forecast what’s coming. They let you extrapolate results from a sample to a larger population.

Here’s the question we’re answering: Would version A or version B perform better when rolled out to your entire audience?

A Quick Example

Let’s say you’re studying Olympic swimmers. With descriptive statistics, you could calculate:

  • Average height of the team
  • Height variance across athletes
  • Distribution above or below average

That’s useful, but limited.

Inferential statistics let you go further. Want to know the average height of all men on the planet? You can’t measure everyone. But you can infer that average from smaller, representative samples.

That’s where Frequentist vs Bayesian methods come in. Both help you make predictions from incomplete data—but they do it differently, especially when applied to A/B testing.

What is the Frequentist Statistics Method in A/B Testing?

The Frequentist approach is the classic. You’ve probably seen it in college stats classes or in most A/B testing tools.

This is one of the main Frequentist vs Bayesian A/B testing comparisons: Frequentist statistics focus on long-run frequencies and fixed hypotheses.

Here’s how it works:

The Hypothesis

You start by assuming there is no difference between version A and version B. This is called the null hypothesis.

At the end of your test, you get a P-Value (probability value). The P-Value tells you the probability of seeing your results—or more extreme results—if there really is no difference between your variations. In other words, how likely is it that your results happened by chance?

The smaller the P-Value, the more confident you can be that there’s a real difference between your A/B testing variations.

Frequentist ProsFrequentist Cons
Fast computation: Frequentist models run quickly and are widely available in any stats library.
No peeking allowed: You can only estimate the P-Value at the end of a test. Looking at results early—called “data peeking”—creates misleading conclusions because it turns one experiment into multiple experiments.
Widely understood: It’s the standard approach taught in most statistics courses and used in many A/B testing tools.No gain estimation: You’ll know which version won, but not by how much. That makes A/B testing business decisions harder.

What is the Bayesian Statistics in A/B Testing?

The Bayesian approach takes a different route—and we think it’s a smarter one for many A/B testing scenarios.

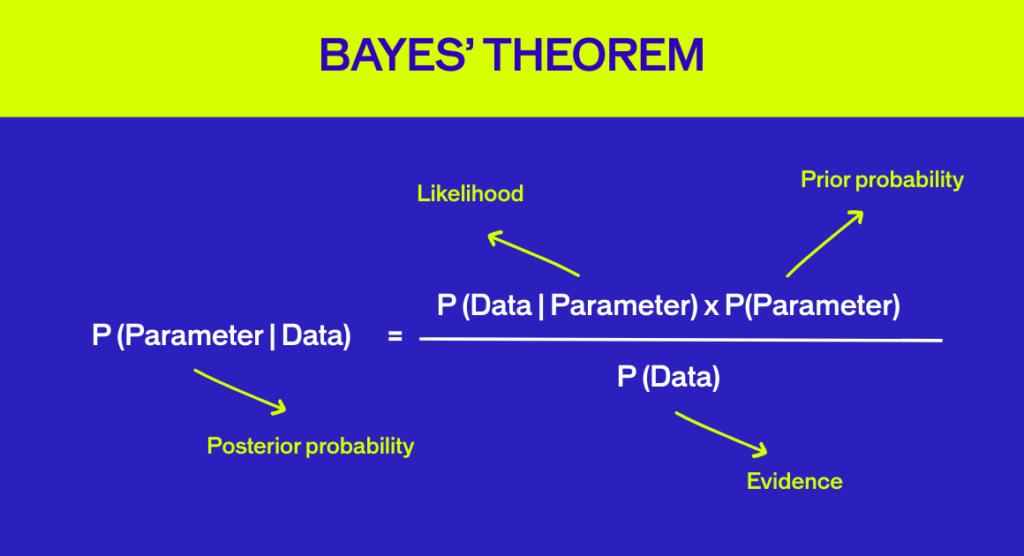
Bayes' Theorem formula

The Bayesian approach allows for the inclusion of prior information (‘a prior’) intNamed after British mathematician Thomas Bayes, this method lets you incorporate prior information into your analysis. It’s built around three overlapping concepts:

The Three Pillars of Bayesian Analysis

  • Prior: Information from previous experiments. At the start, we use a “non-informative” prior—essentially a blank slate.
  • Evidence: The data from your current experiment.
  • Posterior: Updated information combining the prior and evidence. This is your result.

Here’s the game-changer: Bayesian A/B testing is designed for ongoing experiments.  Every time you check your data, the previous results become the “prior,” and new incoming data becomes the “evidence.”

That means data peeking is built into the design. Each time you look, the analysis is valid.

Even better? Bayesian statistics let you estimate the actual gain of a winning variation—not just that it won—making Frequentist vs Bayesian methods in A/B testing very different from a decision-making perspective.

Bayesian ProsBayesian Cons
Peek freely: Check your data during a test without compromising accuracy. Stop losing variations early or switch to winners faster.More computational power: Requires a sampling loop, which demands more CPU load at scale (though this doesn’t affect users).
See the gain: Know the actual improvement range, not just which version won.

Fewer false positives: The method naturally rules out many misleading results in A/B testing.

Frequentist vs Bayesian A/B Testing: The Comparison

Let’s be clear: both methods are statistically valid. But when you compare Frequentist vs Bayesian A/B testing, the practical implications are very different.

At AB Tasty, we have a clear preference for the Bayesian a/b testing approach. 

Here’s why.

Gain Size Matters

With Bayesian A/B testing, you don’t just know which version won—you know by how much.

This is critical in business. When you run an A/B test, you’re deciding whether to switch from version A to version B.

That decision involves:

  • Implementation costs (time, resources, budget)
  • Associated costs (vendor licenses, maintenance)

Example: You’re testing a chatbot on your pricing page. Version B (with chatbot) outperforms version A. But implementing version B requires two weeks of developer time plus a monthly chatbot license.

You need to know if the math adds up. Bayesian statistics give you that answer by quantifying the gain from your A/B testing experiment.

Real Example from AB Tasty Reporting

Let’s look at a test measuring three variations against an original, with “CTA clicks” as the KPI.

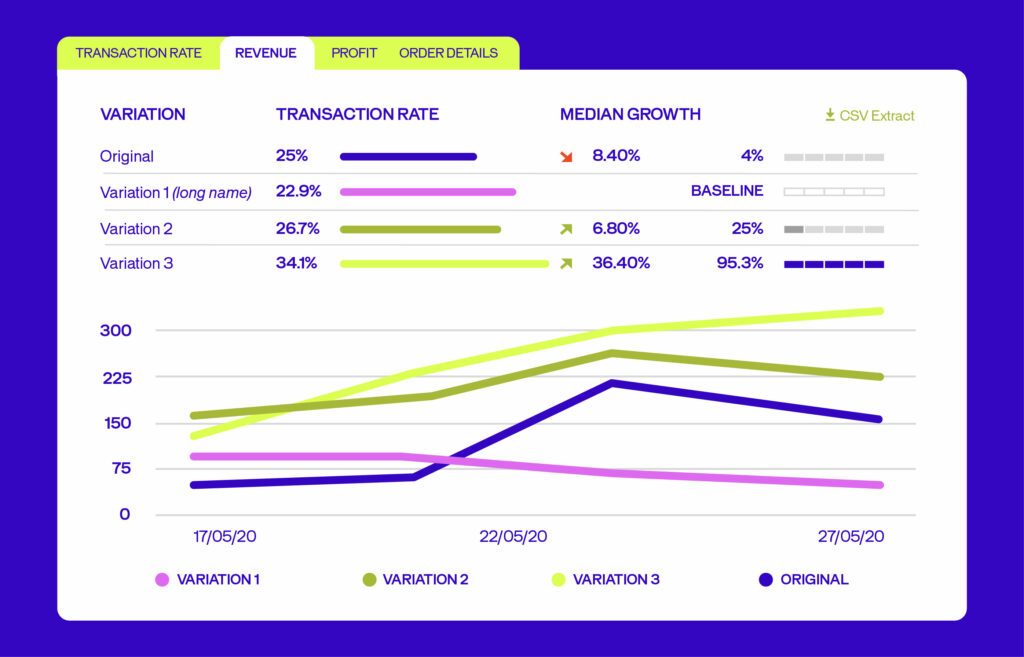
AB testing dashboard showing an example of transaction rates and growth metrics across 4 variations with performance trend graph.

Variation 3 wins with a 34.1% conversion rate (vs. 25% for the original).

But here’s where it gets interesting:

  • Median gain: +36.4%
  • Lowest possible gain: +2.25%
  • Highest possible gain: +48.40%

In 95% of cases, your gain will fall between +2.25% and +48.40%.

This granularity helps you decide whether to roll out the winner:

  • Both ends positive? Great sign.
  • Narrow interval? High confidence. Go for it.
  • Wide interval but low implementation cost? Probably safe to proceed.
  • Wide interval with high implementation cost? Wait for more data.

This is a concrete illustration of how Frequentist vs Bayesian methods in A/B testing lead to different levels of decision-making insight.

When to Trust Your Results?

At AB Tasty, we recommend waiting until you’ve hit these benchmarks:

  • At least 5,000 unique visitors per variation
  • Test runs for at least 14 days (two business cycles)
  • 300 conversions on your main goal

These thresholds apply regardless of whether you use a Frequentist or Bayesian method, but Bayesian A/B testing gives you more interpretable outputs once you reach them.

Data Peeking: A Bayesian Advantage

Here’s a scenario: You’re running an A/B test for a major e-commerce promotion. Version B is tanking—losing you serious money.

With Bayesian A/B testing, you can stop it immediately. No need to wait until the end.

Conversely, if version B is crushing it, you can switch all traffic to the winner earlier than with Frequentist methods.

This is the logic behind our Dynamic Traffic Allocation feature—and it wouldn’t be possible without Bayesian statistics.

How Does Dynamic Traffic Allocation Work?

Dynamic Traffic Allocation balances exploration (gathering data) with exploitation (maximizing conversions).

AB Tasty traffic allocation interface with slider controls and pie chart showing test split between original and variations.

In practice, you simply:

  • Check the Dynamic Traffic Allocation box.
  • Pick your primary KPI.
  • Let the algorithm decide when to send more traffic to the winner.

This approach shines when:

  • Testing micro-conversions over short periods
  • Running time-limited campaigns (holiday sales, flash promotions)
  • Working with low-traffic pages
  • Testing 6+ variations simultaneously

Again, this is where Frequentist vs Bayesian methods in A/B testing diverge: Frequentist statistics are not naturally designed for safe continuous monitoring and dynamic allocation in the same way.

Bayesian False Positives Explained

A false positive occurs when test results suggest version B improves performance—but in reality, it doesn’t. Often, version B performs the same as version A, not worse.

False positives happen with both Frequentist and Bayesian methods in A/B testing. But here’s the difference:

How Does Bayesian Testing Limit False Positives?

Because Bayesian A/B testing provides a gain interval, you’re less likely to implement a false positive in the first place.

Example: Your test shows version B wins with 95% confidence, but the median improvement is only 1%. Even if this is a false positive, you probably won’t implement it—the resources needed don’t justify such a small gain.

With Frequentist methods, you don’t see the gain interval. You might implement that false positive, wasting time and energy on changes that bring zero return.

Gain probability using Bayesian statistics

The standard rule of thumb is 95% confidence—you’re 95% sure version B performs as indicated, with a 5% risk it doesn’t.

For most campaigns, 95% confidence works just fine. But when the stakes are high—think major product launches or business-critical tests—you can dial up your confidence threshold to 97%, 98%, or even 99%.

Just know this: whether you’re using Frequentist or Bayesian methods, higher confidence means you’ll need more time and traffic to reach statistical significance. It’s a trade-off worth making when precision matters most.

While this seems like a safe bet – and it is the right choice for high-stakes campaigns – it’s not something to apply across the board.

This is because:

  • In order to attain this higher threshold, you’ll have to wait longer for results, therefore leaving you less time to reap the rewards of a positive outcome.
  • You will implicitly only get a winner with a bigger gain (which is rarer), and you will let go of smaller improvements that still could be impactful.
  • If you have a smaller amount of traffic on your web page, you may want to consider a different approach.

Conclusion

So which is better—Frequentist or Bayesian?

Both are sound statistical methods. But when you look at Frequentist vs Bayesian methods in A/B testing, we’ve chosen the Bayesian approach because it helps teams make better business decisions.

Here’s what you get:

  • Flexibility: Peek at data without compromising accuracy.
  • Actionable insights: Know the gain size, not just the winner.
  • Maximized returns: Dynamic Traffic Allocation optimizes automatically.
  • Fewer false positives: Built-in safeguards against misleading results.

When you’re shopping for an A/B testing platform, find one that gives you results you can trust—and act on.

Want to see Bayesian A/B testing in action? AB Tasty makes it easy to set up tests, gather insights via an ROI dashboard, and determine which changes will increase your revenue. 

Ready to go further? Let’s build better experiences together →

FAQs

What’s the main difference between Bayesian and Frequentist A/B testing?

When you compare Frequentist vs Bayesian methods in A/B testing, Frequentist methods test whether there’s a difference between variations using a P-Value at the end of the experiment. Bayesian methods estimate the size of the gain and let you update results continuously as new data comes in.

Can I peek at my A/B test results early?

With Bayesian A/B testing, yes. The method is designed for ongoing analysis. With Frequentist methods, peeking early creates misleading results because it effectively turns one experiment into multiple experiments.

What is a false positive in A/B testing?

A false positive occurs when test results suggest version B improves performance, but in reality it doesn’t. Bayesian methods help limit false positives by showing the gain interval, making it less likely you’ll implement a variation with minimal or no real improvement.

What confidence level should I use for my A/B tests?

95% confidence is standard for most marketing campaigns. For high-stakes A/B testing, you can increase to 97%, 98%, or 99%—but this requires more time and traffic to reach statistical significance, regardless of whether you use Frequentist or Bayesian methods.

How long should I run my A/B test?

At AB Tasty, we recommend running tests for at least 14 days (two business cycles) and collecting at least 5,000 unique visitors per variation and 300 conversions on your main goal. These benchmarks help both Frequentist and Bayesian approaches produce reliable insights.

What is Dynamic Traffic Allocation?

Dynamic Traffic Allocation is an automated feature that balances data exploration with conversion maximization in A/B testing. Once the algorithm identifies a winning variation with confidence, it automatically sends more traffic to that version—helping you maximize returns while still gathering reliable data using Bayesian methods.

Share on

LinkedIn Facebook Twitter

Article

Oct 23, 2025
6min read

Mastering Revenue Metrics: Understand the Power and Practical Use of RevenueIQ

Hubert Wassner

Hubert Wassner

Revenue is the cornerstone of any e-commerce business, yet most optimization efforts focus only on improving conversion rates.

Average Order Value (AOV), an equally important driver of revenue, is often overlooked because it’s difficult to measure accurately with standard statistical tools. This gap can lead to missed opportunities and slow decision-making.

RevenueIQ addresses this challenge by providing a robust, reliable way to measure and optimize revenue directly—combining conversion and AOV into a single, actionable metric.

Here’s how RevenueIQ changes the way you approach experimentation and business growth.

Discover how to accurately measure and optimize revenue in your experiments with our patented feature.

The most important KPI in e-commerce is revenue. In an optimization context, this means focusing on two key areas:

  • Conversion Rate (CR): Turning as many visitors as possible into customers.
  • Average Order Value (AOV): Generating as much value as possible per customer.

However, Conversion Rate Optimization (CRO) often remains focused on conversion, while AOV is frequently neglected due to its statistical complexity. Accurately estimating AOV with classic tests (such as the t-test or Mann-Whitney) is challenging because purchase distributions are highly skewed and have no upper bound.

RevenueIQ offers a robust test that directly estimates the distribution of the effect on revenue (through a refined estimation of AOV), providing both the probability of gain (“chance to win”) and consistent confidence intervals.

In benchmarks, RevenueIQ maintains a correct false positive rate, has power close to Mann-Whitney, and produces confidence intervals four times narrower than the t-test. By combining the effects of AOV and CR, it delivers an RPV (Revenue Per Visitor) impact and then an actionable revenue projection.

Curious to learn more details? Please read our RevenueIQ Whitepaper for a full scientific explanation written by our Data Scientist, Hubert Wassner.

Context & Problem

In CRO, we often optimize CR due to a lack of suitable tools for revenue. Yet, Revenue = Visitors × CR × AOV; ignoring AOV distorts the view.

AOV is misleading because:

  • It is unbounded (someone can buy many items).
  • It is highly right-skewed (many small orders, a few very large ones).
  • A few “large and rare” values can dominate the average.
  • In random A/B splits, these large orders can be unevenly distributed, leading to huge variance in observed AOV.

Limitations of Classic Tests

t-test

Assumes normality (or relies on the Central Limit Theorem for the mean). On highly skewed e-commerce data, the CLT variance formula is unreliable at realistic volumes. The result: very low power (detects ~15% of true winners in the benchmark) and very wide confidence intervals, leading to slow and imprecise decisions.

Mann-Whitney (MW):

Robust to non-normality (works on ranks), so much more powerful (~80% detection in the benchmark). But it only provides a p-value (thus only trend information), not an estimate of effect size (no confidence interval), making it impossible to quantify the business case.

RevenueIQ: Principle

It uses and combines two innovative approaches:

  1. Bootstrap Technique: Studies the variability of a measure with unknown statistical behavior.
  2. Basket Difference Measurement: Instead of measuring the difference in average baskets, it measures the average of basket differences. It compares sorted order differences between variants (A and B), with weighting by density (approx. log-normal) to favor “comparable” pairs. This bypasses the problem of very large observed value differences in such data.

RevenueIQ then provides:

  • The Chance to Win (probability that the effect is > 0), which is easy for decision-makers to interpret.
  • Narrow and reliable confidence intervals on the AOV effect as well as on revenue.

Benchmarks (AOV)

  • Alpha validity (on AA tests): Good control of false positives. Using a typical 95% threshold exposes only a 5% false positive risk.
  • Statistical power measurement: 1000 AB tests with a known effect of +€5
    • MW Test: 796/1000 winners, ~80% power.
    • t-test: 146/1000, only 15% power.
    • RevenueIQ: 793/1000 (≈ equivalent to MW). ~80% power.
  • Confidence interval (CI): RevenueIQ produces CIs of €8 width, which is reasonable and functional in the context of a real effect of €5. With an average CI width of €34, the t-test is totally ineffective.
  • CI coverage: The validity of the confidence intervals was verified. A 95% CI indeed has a 95% chance of containing the true effect value (i.e., €0 for AA tests and €5 for AB tests).

From AOV KPI to Revenue

Beyond techniques and formulas, the key point is that RevenueIQ uses a Bayesian method for AOV analysis, allowing this metric to be merged with conversion. Competitors use frequentist methods, at least for AOV, making any combination of results impossible. Under the hood, RevenueIQ combines conversion and AOV results into a central metric: visitor value (RPV). With precise knowledge of RPV, revenue (in € or other currency) is then projected by multiplying by the targeted traffic for a given period.

Real Case (excerpt) Here is a textbook case for RevenueIQ:

  • Conversion gain is 92% CTW, encouraging but not “significant” by standard threshold.
  • AOV gain is at 80% CTW. Similarly, taken separately, this is not enough to declare a winner.
  • The combination of these two metrics gives a CTW of 95.9% for revenue, enabling a simple and immediate decision, where a classic approach would have required additional data collection while waiting for one of the two KPIs (CR or AOV) to become significant.
  • For an advanced business decision, RevenueIQ provides an estimated average gain of +€50k, with a confidence interval [-€6,514; +€107,027], allowing identification of minimal risk and substantial gain.

What This Changes for Experimentation

  • Without RevenueIQ: “inconclusive” results (or endless tests) lead to missed opportunities.
  • With RevenueIQ: Faster, quantified decisions (probability, effect, CI), at the revenue level (RPV then projected revenue).

Practical Recommendations

  • Stop interpreting observed AOV without safeguards: it is highly volatile.
  • Avoid filtering/Winsorizing “extreme values”: arbitrary thresholds ⇒ bias.
  • Measure CR & AOV jointly and reason in RPV to reflect business reality.
  • Use RevenueIQ to obtain chance to win + CI on AOV, RPV, and revenue projection.
  • Decide via projected revenue (average gain, lower CI bound) rather than isolated p-values.

Curious to learn more details? Please read our RevenueIQ Whitepaper for a full scientific explanation written by our Data Scientist, Hubert Wassner.

Conclusion

RevenueIQ brings a robust and quantitative statistical test to monetary metrics (AOV, RPV, revenue), where:

  • t-test is weak and imprecise on e-commerce data,
  • Mann-Whitney is powerful but not quantitative.

RevenueIQ enables faster detection, quantification of business impact, and prioritization of deployments with explicit confidence levels.

**Original information can be found by following this link to AB Tasty’s documentation, “Understanding the practical use of RevenueIQ.”

Share on

LinkedIn Facebook Twitter

Article

Jul 11, 2025
7min read

Is Your Average Order Value (AOV) Misleading You?

Hubert Wassner

Hubert Wassner

Average Order Value (AOV) is a widely used metric in Conversion Rate Optimization (CRO), but it can be surprisingly deceptive. While the formula itself is simple—summing all order values and dividing by the number of orders—the real challenge lies within the data itself.

The problem with averaging

AOV is not a “democratic” measure. A single high-spending customer can easily spend 10 or even 100 times more than your average customer. These few extreme buyers can heavily skew the average, giving a limited number of visitors disproportionate impact compared to hundreds or thousands of others. This is problematic because you can’t truly trust the significance of an observed AOV effect if it’s tied to just a tiny fraction of your audience.

Let’s look at a real dataset to see just how strong this effect can be. Consider the order value distribution:

  • The horizontal axis represents the order value.
  • The vertical axis represents the frequency of that order value.
  • The blue surface is a histogram, while the orange outline is a log-normal distribution approximation.

This graph shows that the most frequent order values are small, around €20. As the order value increases, the frequency of such orders decreases. This is a “long/heavy tail distribution,” meaning very large values can occur, albeit rarely.

A single strong buyer with an €800 order value is worth 40 times more than a frequent buyer when looking at AOV. This is an issue because a slight change in the behavior of 40 visitors is a stronger indicator than a large change from one unique visitor. While not fully visible on this scale, even more extreme buyers exist. 

The next graph, using the same dataset, illustrates this better:

  • The horizontal axis represents the size of the growing dataset of order values (roughly indicating time).
  • The vertical axis represents the maximum order value in the growing dataset in €

At the beginning of data collection, the maximum order value is quite small (close to the most frequent value of ~€20). However, we see that it grows larger as time passes and the dataset expands. With a dataset of 10,000 orders, the maximum order value can exceed €5,000. This means any buyer with an order above €5,000 (they might have multiple) holds 250 times the power of a frequent buyer at €20. At the maximum dataset size, a single customer with an order over €20,000 can influence the AOV more than 2,000 other customers combined.

When looking at your e-commerce metrics, AOV should not be used as a standalone decision-making data.

E-commerce moves fast. Get the insights that help you move faster. Download the 2025 report now.

GET THE REPORT

The challenge of AB Test splitting

The problem intensifies when considering the random splits used in A/B tests.

Imagine you have only 10 very large spenders whose collective impact equals that of 10,000 medium buyers. There’s a high probability that the random split for such a small group of users will be uneven. While the overall dataset split is statistically even, the disproportionate impact of these high spenders on AOV requires specific consideration for this small segment. Since you can’t predict which visitor will become a customer or how much they will spend, you cannot guarantee an even split of these high-value users.

This phenomenon can artificially inflate or deflate AOV in either direction, even without a true underlying effect, simply depending on which variation these few high spenders land on.

What’s the solution?

AOV is an unreliable metric, how can we effectively work with it? The answer is similar to how you approach conversion rates and experimentation.

You don’t trust raw conversion data—one more conversion on variation B doesn’t automatically make it a winner, nor do 10 or 100. Instead, you rely on a statistical test to determine when a difference is significant. The same principle applies to AOV. Tools like AB Tasty offer the Mann-Whitney test, a statistical method robust against extreme values and well-suited for long-tail distributions.

AOV behavior can be confusing because you’re likely accustomed to the more intuitive statistics of conversion rates. Conversion data and their corresponding statistics usually align; a statistically significant increase in conversion rate typically means a visibly large difference in the number of conversions, consistent with the statistical test. However, this isn’t always the case with AOV. It’s not uncommon to see the AOV trend and the statistical results pointing in different directions. Your trust should always be placed in the statistical test.

The root cause: Heavy tail distributions

You now understand that the core issue stems from the unique shape of order value distributions: long-tail distributions that produce rare, extreme values.

It’s important to note that the problem isn’t just the existence of extreme values. If these extreme values were frequent, the AOV would naturally be higher, and their impact would be less dramatic because the difference between the AOV and these values would be smaller. Similarly, for the splitting problem, a larger number of extreme values would ensure a more even split.

At this point, you might think your business has a different order distribution shape and isn’t affected. However, this shape emerges whenever these two conditions are met:

  • You have a price list with more than several dozen different values.
  • Visitors can purchase multiple products at once.

Needless to say, these conditions are ubiquitous and apply to nearly every e-commerce business. The e-commerce revolution itself was fueled by the ability to offer vast catalogues.

Furthermore, the presence of shipping costs naturally encourages users to group their purchases to minimize those costs. It means that nearly all e-commerce businesses are affected. The only exceptions are subscription-based businesses with limited pricing options, where most purchases are for a single service.

Here’s a glimpse into the order value distribution across various industries, demonstrating the pervasive nature of the “long tail distribution”:

Cosmetic
Transportation
B2B packaging (selling packaging for e-commerce)
Fashion
online flash sales

AOV, despite its simple definition and apparent ease of understanding, is a misleading metric. Its magnitude is easy to grasp, leading people to confidently make intuitive decisions based on its fluctuations. However, the reality is far more complex; AOV can show dramatic changes even when there’s no real underlying effect.

Conversely, significant changes can go unnoticed. A strong negative effect could be masked by just a few high-spending customers landing in a poorly performing variation. So, now you know: just as you do for conversion rates, rely on statistical tests for your AOV decisions.

Share on

LinkedIn Facebook Twitter

Article

May 6, 2025
6min read

Minimal Detectable Effect: The Essential Ally for Your A/B Tests

Hubert Wassner

Hubert Wassner

In CRO (Conversion Rate Optimization), a common dilemma is not knowing what to do with a test that shows a small and non-significant gain. 

Should we declare it a “loser” and move on? Or should we collect more data in the hope that it will reach the set significance threshold? 

Unfortunately, we often make the wrong choice, influenced by what is called the “sunk cost fallacy.” We have already put so much energy into creating this test and waited so long for the results that we don’t want to stop without getting something out of this work. 

However, CRO’s very essence is experimentation, which means accepting that some experiments will yield nothing. Yet, some of these failures could be avoided before even starting, thanks to a statistical concept: the MDE (Minimal Detectable Effect), which we will explore together.

MDE: The Minimal Detectable Threshold

In statistical testing, samples have always been valuable, perhaps even more so in surveys than in CRO. Indeed, conducting interviews to survey people is much more complex and costly than setting up an A/B test on a website. Statisticians have therefore created formulas that link the main parameters of an experiment for planning purposes:

  • The number of samples (or visitors) per variation
  • The baseline conversion rate
  • The magnitude of the effect we hope to observe

This allows us to estimate the cost of collecting samples. The problem is that, among these three parameters, only one is known: the baseline conversion rate. 

We don’t really know the number of visitors we’ll send per variation. It depends on how much time we allocate to data collection for this test, and ideally, we want it to be as short as possible. 

Finally, the conversion gain we will observe at the end of the experiment is certainly the biggest unknown, since that’s precisely what we’re trying to determine.

So, how do we proceed with so many unknowns? The solution is to estimate what we can using historical data. For the others, we create several possible scenarios:

  • The number of visitors can be estimated from past traffic, and we can make projections in weekly blocks.
  • The conversion rate can also be estimated from past data.
  • For each scenario configuration from the previous parameters, we can calculate the minimal conversion gains (MDE) needed to reach the significance threshold.

For example, with traffic of 50,000 visitors and a conversion rate of 3% (measured over 14 days), here’s what we get:

MDE Uplift
  • The horizontal axis indicates the number of days.
  • The vertical axis indicates the MDE corresponding to the number of days.

The leftmost point of the curve tells us that if we achieve a 10% conversion gain after 14 days, then this test will be a winner, as this gain can be considered significant. Typically, it will have a 95% chance of being better than the original. If we think the change we made in the variation has a chance of improving conversion by ~10% (or more), then this test is worth running, and we can hope for a significant result in 14 days.

On the other hand, if the change is minor and the expected gain is less than 10%, then 14 days will not be enough. To find out more, we move the curve’s slider to the right. This corresponds to adding days to the experiment’s duration, and we then see how the MDE evolves. Naturally, the MDE curve decreases: the more data we collect, the more sensitive the test becomes to smaller effects.

For example, by adding another week, making it a 21-day experiment, we see that the MDE drops to 8.31%. Is that sufficient? If so, we can validate the decision to create this experiment.

MDE Graph

If not, we continue to explore the curve until we find a value that matches our objective. Continuing along the curve, we see that a gain of about 5.44% would require waiting 49 days.

Minimum Detectable Uplift Graph

That’s the time needed to collect enough data to declare this gain significant. If that’s too long for your planning, you’ll probably decide to run a more ambitious test to hope for a bigger gain, or simply not do this test and use the traffic for another experiment. This will prevent you from ending up in the situation described at the beginning of this article, where you waste time and energy on an experiment doomed to fail.

From MDE to MCE

Another approach to MDE is to see it as MCE: Minimum Caring Effect. 

This doesn’t change the methodology except for the meaning you give to the definition of your test’s minimal sensitivity threshold. So far, we’ve considered it as an estimate of the effect the variation could produce. But it can also be interesting to consider the minimal sensitivity based on its operational relevance: the MCE. 

For example, imagine you can quantify the development and deployment costs of the variation and compare it to the conversion gain over a year. You could then say that an increase in the conversion rate of less than 6% would take more than a year to cover the implementation costs. So, even if you have enough traffic for a 6% gain to be significant, it may not have operational value, in which case it’s pointless to run the experiment beyond the duration corresponding to that 6%.

MDE graph

In our case, we can therefore conclude that it’s pointless to go beyond 42 days of experimentation because beyond that duration, if the measured gain isn’t significant, it means the real gain is necessarily less than 6% and thus has no operational value for you.

Conclusion

AB Tasty’s MDE calculator feature will allow you to know the sensitivity of your experimental protocol based on its duration. It’s a valuable aid when planning your test roadmap. This will allow you to make the best use of your traffic and resources.

Looking for a free and minimalistic MDE calculator to try? Check out our free Minimal Detectable Effect calculator here.

Share on

LinkedIn Facebook Twitter

Article

Jul 18, 2024
4min read

Transaction Testing With AB Tasty’s Report Copilot

Hubert Wassner

Hubert Wassner

Transaction testing, which focuses on increasing the rate of purchases, is a crucial strategy for boosting your website’s revenue. 

To begin, it’s essential to differentiate between conversion rate (CR) and average order value (AOV), as they provide distinct insights into customer behavior. Understanding these metrics helps you implement meaningful changes to improve transactions.

In this article, we’ll delve into the complexities of transaction metrics analysis and introduce our new tool, the “Report Copilot,” designed to simplify report analysis. Read on to learn more.

Transaction Testing

To understand how test variations impact total revenue, focus on two key metrics:

  • Conversion Rate (CR): This metric indicates whether sales are increasing or decreasing. Tactics to improve CR include simplifying the buying process, adding a “one-click checkout” feature, using social proof, or creating urgency through limited inventory.
  • Average Order Value (AOV): This measures how much each customer is buying. Strategies to enhance AOV include cross-selling or promoting higher-priced products.

By analyzing CR and AOV separately, you can pinpoint which metrics your variations impact and make informed decisions before implementation. For example, creating urgency through low inventory may boost CR but could reduce AOV by limiting the time users spend browsing additional products. After analyzing these metrics individually, evaluate their combined effect on your overall revenue.

Revenue Calculation

The following formula illustrates how CR and AOV influence revenue:

Revenue=Number of Visitors×Conversion Rate×AOV

In the first part of the equation (Number of Visitors×Conversion Rate), you determine how many visitors become customers. The second part (×AOV) calculates the total revenue from these customers.

Consider these scenarios:

  • If both CR and AOV increase, revenue will rise.
  • If both CR and AOV decrease, revenue will fall.
  • If either CR or AOV increases while the other remains stable, revenue will increase.
  • If either CR or AOV decreases while the other remains stable, revenue will decrease.
  • Mixed changes in CR and AOV result in unpredictable revenue outcomes.

The last scenario, where CR and AOV move in opposite directions, is particularly complex due to the variability of AOV. Current statistical tools struggle to provide precise insights on AOV’s overall impact, as it can experience significant random fluctuations. For more on this, read our article “Beyond Conversion Rate.”

While these concepts may seem intricate, our goal is to simplify them for you. Recognizing that this analysis can be challenging, we’ve created the “Report Copilot” to automatically gather and interpret data from variations, offering valuable insights.

Report Copilot

The “Report Copilot” from AB Tasty automates data processing, eliminating the need for manual calculations. This tool empowers you to decide which tests are most beneficial for increasing revenue.

Here are a few examples from real use cases.

Winning Variation:

The left screenshot provides a detailed analysis, helping users draw conclusions about their experiment results. Experienced users may prefer the summarized view on the right, also available through the Report Copilot.

Complex Use Case:


The screenshot above demonstrates a case where CR and OAV have opposite trends and need a deeper understanding of the context.

It’s important to note that the Report Copilot doesn’t make decisions for you; it highlights the most critical parts of your analysis, allowing you to make informed choices.

Conclusion

Transaction analysis is complex, requiring a breakdown of components like conversion rate and average order value to better understand their overall effect on revenue. 

We’ve developed the Report Copilot to assist AB Tasty users in this process. This feature leverages AB Tasty’s extensive experimentation dashboard to provide comprehensive, summarized analyses, simplifying decision-making and enhancing revenue strategies.

Share on

LinkedIn Facebook Twitter

Article

May 23, 2024
5min read

Mutually Exclusive Experiments: Preventing the Interaction Effect

Hubert Wassner

Hubert Wassner

What is the interaction effect?

If you’re running multiple experiments at the same time, you may find their interpretation to be more difficult because you’re not sure which variation caused the observed effect. Worse still, you may fear that the combination of multiple variations could lead to a bad user experience.

It’s easy to imagine a negative cumulative effect of two visual variations. For example, if one variation changes the background color, and another modifies the font color, it may lead to illegibility. While this result seems quite obvious, there may be other negative combinations that are harder to spot.

Imagine launching an experiment that offers a price reduction for loyal customers, whilst in parallel running another that aims to test a promotion on a given product. This may seem like a non-issue until you realize that there’s a general rule applied to all visitors, which prohibits cumulative price reductions – leading to a glitch in the purchase process. When the visitor expects two promotional offers but only receives one, they may feel frustrated, which could negatively impact their behavior.

What is the level of risk?

With the previous examples in mind, you may think that such issues could be easily avoided. But it’s not that simple. Building several experiments on the same page becomes trickier when you consider code interaction, as well as interactions across different pages. So, if you’re interested in running 10 experiments simultaneously, you may need to plan ahead.

A simple solution would be to run these tests one after the other. However, this strategy is very time consuming, as your typical experiment requires two weeks to be performed properly in order to sample each day of the week twice.

It’s not uncommon for a large company to have 10 experiments in the pipeline and running them sequentially will take at least 20 weeks. A better solution would be to handle the traffic allocated to each test in a way that renders the experiments mutually exclusive.

This may sound similar to a multivariate test (MVT), except the goal of an MVT is almost the opposite: to find the best interaction between unitary variations.

Let’s say you want to explore the effect of two variation ideas: text and background color. The MVT will compose all combinations of the two and expose them simultaneously to isolated chunks of the traffic. The isolation part sounds promising, but the “all combinations” is exactly what we’re trying to avoid. Typically, the combination of the same background color and text will occur. So an MVT is not the solution here.

Instead, we need a specific feature: A Mutually Exclusive Experiment.

What is a Mutually Exclusive Experiment (M2E)?

AB Tasty’s Mutually Exclusive Experiment (M2E) feature enacts an allocation rule that blocks visitors from entering selected experiments depending on the previous experiments already displayed. The goal is to ensure that no interaction effect can occur when a risk is identified.

How and when should we use Mutually Exclusive Experiments?

We don’t recommend setting up all experiments to be mutually exclusive because it reduces the number of visitors for each experiment. This means it will take longer to achieve significant results and the detection power may be less effective.

The best process is to identify the different kinds of interactions you may have and compile them in a list. If we continue with the cumulative promotion example from earlier, we could create two M2E lists: one for user interface experiments and another for customer loyalty programs. This strategy will avoid negative interactions between experiments that are likely to overlap, but doesn’t waste traffic on hypothetical interactions that don’t actually exist between the two lists.

What about data quality?

With the help of an M2E, we have prevented any functional issues that may arise due to interactions, but you might still have concerns that the data could be compromised by subtle interactions between tests.

Would an upstream winning experiment induce false discovery on downstream experiments? Alternatively, would a bad upstream experiment make you miss an otherwise downstream winning experiment? Here are some points to keep in mind:

  • Remember that roughly eight tests out of 10 are neutral (show no effect), so most of the time you can’t expect an interaction effect – if no effect exists in the first place.
  • In the case where an upstream test has an effect, the affected visitors will still be randomly assigned to the downstream variations. This evens out the effect, allowing the downstream experiment to correctly measure its potential lift. It’s interesting to note that the average conversion rate following an impactful upstream test will be different, but this does not prevent the downstream experiment from correctly measuring its own impact.
  • Remember that the statistical test is here to take into account any drift of the random split process. The drift we’re referring to here is the fact that more impacted visitors of the upstream test could end up in a given variation creating the illusion of an effect on the downstream test. So the gain probability estimation and the confidence interval around the measured effect is informing you that there is some randomness in the process. In fact, the upstream test is just one example among a long list of possible interfering events – such as visitors using different computers, different connection quality, etc.

All of these theoretical explanations are supported by an empirical study from the Microsoft Experiment Platform team. This study reviewed hundreds of tests on millions of visitors and saw no significant difference between effects measured on visitors that saw just one test and visitors that saw an additional upstream test.

Conclusion

While experiment interaction is possible in a specific context, there are preventative measures that you may take to avoid functional loss. The most efficient solution is the Mutually Exclusive Experiment, allowing you to eliminate the functional risks of simultaneous experiments, make the most of your traffic and expedite your experimentation process.

References:

https://www.microsoft.com/en-us/research/group/experimentation-platform-exp/articles/a-b-interactions-a-call-to-relax/

 

Share on

LinkedIn Facebook Twitter

Article

May 14, 2024
6min read

The Truth Behind the 14-Day A/B Test Period

Hubert Wassner

Hubert Wassner

The A/B testing method involves a simple process: create two variations, expose them to your customer, collect data, and analyze the results with a statistical formula. 

But, how long should you wait before collecting data? With 14 days being standard practice, let’s find out why as well as any exceptions to this rule.

Why 14 days?

To answer this question we need to understand what we are fundamentally doing. We are collecting current data within a short window, in order to forecast what could happen in the future during a more extended period. To simplify this article, we will only focus on explaining the rules that relate to this principle. Other rules do exist, which mostly correlate to the number of visitors, but this can be addressed in a future article.

The forecasting strategy relies on the collected data containing samples of all event types that may be encountered in the future. This is impossible to fulfill in practice, as periods like Christmas or Black Friday are exceptional events relative to the rest of the year. So let’s focus on the most common period and set aside these special events that merit their own testing strategies.

If the future we are considering relates to “normal” times, our constraint is to sample each day of the week uniformly, since people do not behave the same on different days. Simply look at how your mood and needs shift between weekdays and weekends. This is why a data sampling period must include entire weeks, to account for fluctuations between the days of the week. Likewise, if you sample eight days for example, one day of the week will have a doubled impact, which doesn’t realistically represent the future either.

This partially explains the two-week sampling rule, but why not a longer or shorter period? Since one week covers all the days of the week, why isn’t it enough? To understand, let’s dig a little deeper into the nature of conversion data, which has two dimensions: visits and conversions.

  • Visits: as soon as an experiment is live, every new visitor increments the number of visits.
  • Conversions: as soon as an experiment is live, every new conversion increments the number of conversions.

It sounds pretty straightforward, but there is a twist: statistical formulas work with the concept of success and failure. The definition is quite easy at first: 

  • Success: the number of visitors that did convert.
  • Failures: the number of visitors that didn’t convert.

At any given time a visitor may be counted as a failure, but this could change a few days later if they convert, or the visit may remain a failure if the conversion didn’t occur. 

So consider these two opposing scenarios: 

  • A visitor begins his buying journey before the experiment starts. During the first days of the experiment he comes back and converts. This would be counted as a “success”, but in fact he may not have had time to be impacted by the variation because the buying decision was made before he saw it. The problem is that we are potentially counting a false success: a conversion that could have happened without the variation.
  • A visitor begins his buying journey during the experiment, so he sees the variation from the beginning, but doesn’t make a final decision before the end of the experiment – finally converting after it finishes. We missed this conversion from a visitor who saw the variation and was potentially influenced by it.

These two scenarios may cancel each other out since they have opposite results, but that is only true if the sample period exceeds the usual buying journey time. Consider a naturally long conversion journey, like buying a house, measured within a very short experiment period of one week. Clearly, no visitors beginning the buying journey during the experiment period would have time to convert. The conversion rates of these visitors would be artificially in the realm of zero – no proper measurements could be done in this context. In fact, the only conversions you would see are the ones from visitors that began their journey before the variation even existed. Therefore, the experiment would not be measuring the impact of the variation. 

The delay between the effective variation and the conversion expedites the conversion rate. In order to mitigate this problem, the experiment period has to be twice as long as the standard conversion journey. Doing so ensures that visitors entering the experiment during the first half will have time to convert. You can expect that people who began their journey before the experiment and people entering during the second half of the experiment period will cancel each other out: The first group will contain conversions that should not be counted, and some of the second group’s conversions will be missing. However, a majority of genuine conversions will be counted.

That’s why a typical buying journey of one week results in a two-week experiment, offering the right balance in terms of speed and accuracy of the measurements.

Exceptions to this rule

A 14-day experiment period doesn’t apply to all cases. If the delay between the exposed variation and the conversion is 1.5 weeks for instance, then your experiment period should be three weeks, in order to cover the usual conversion delay twice. 

On the other hand, if you know that the delay is close to zero, such as in the case of a media website, where you are trying to optimize the placement of an advertisement frame on a page where visitors only stay a few minutes, you may think that one day would be enough based on the this logic, but it’s not. 

The reason being that you would not sample every day of the week, and we know from experience that people do not behave the same way throughout the week. So even in a zero-delay context, you still need to conduct the experiment for an entire week.

Takeaways: 

  1. Your test period should mirror the conditions of your expected implementation period.
  2. Sample each day of the week in the same way.
  3. Wait an integer number of weeks before closing an A/B test.

Respecting these rules will ensure that you’ll have clean measures. The accuracy of the measure is defined by another parameter of the experiment: the total number of visitors. We’ll address this topic in another article – stay tuned.

Share on

LinkedIn Facebook Twitter

Article

Mar 4, 2024
8min read

Optimizing Revenue Beyond Conversion Rate

Hubert Wassner

Hubert Wassner

When it comes to CRO, or Conversion Rate Optimization, it would be natural to assume that conversion is all that matters. At least, we can argue that conversion rate is at the heart of most experiments. However, the ultimate goal is to raise revenue, so why does the CRO world put so much emphasis on conversion rates?

In this article, we’ll shed some light on the reason why conversion rate is important and why it’s not just conversions that should be considered.

Why is conversion rate so important?

Let’s start off with the three technical reasons why CRO places such importance on conversion rates:

  1. Conversion is a generic term. It covers the fact that an e-commerce visitor becomes a customer by buying something, or simply the fact that this visitor went farther than just the homepage, or clicks on a product page, or adds this product to the cart. In that sense, it’s the Swiss Army Knife of CRO.
  2. Conversion statistics are far easier than other KPI statistics, and they’re the simplest from a maths point of view. In terms of measurement, it’s pretty straightforward: success or failure.
    This means off-the-shelf code or simple spreadsheet formulas can compute statistics indices for decision, like the chance to win or confidence intervals about the expected gain. This is not that easy for other metrics as we will see later with Average Order Value (AOV).
  3. Conversion analysis is also the simplest when it comes to decision-making. There’s (almost) no scenario where raising the number of conversions is a bad thing. Therefore, deciding whether or not to put a variation in production is an easy task when you know that the conversion rate will rise. The same can’t be said about the “multiple conversions” metric where, unlike the conversion rate metric that counts one conversion per visitor even if this visitor made 2 purchases, every conversion counts and so is often more complex to analyze. For example, the number of product pages seen by an e-commerce visitor is harder to interpret. A variation increasing this number could have several meanings: the catalog can be seen as more engaging or it could mean that visitors are struggling to find what they’re looking for. 

Due to the aforementioned reasons, the conversion rate is the starting point of all CRO journeys. However, conversion rate on its own is not enough. It’s also important to pay attention to other factors other than conversions to optimize revenue. 

Beyond conversion rate

Before we delve into a more complex analysis, we’ll take a look at some simpler metrics. This includes ones that are not directly linked to transactions such as “add to cart” or “viewed at least one product page”.

If it’s statistically assured to win, then it’s a good choice to put the variation into production, with one exception. If the variation is very costly, then you will need to dig deeper to ensure that the gains will cover the costs. This can occur, for example, if the variation holds a product recommender system that comes with its cost. 

The bounce rate is also simple and straightforward in that the aim is to keep the figure down unlike the conversion rate. In this case, the only thing to be aware of is that you want to lower the bounce rate unlike the conversion rate. But the main idea is the same: if you change your homepage image and you see the bounce rate statistically drop, then it’s a good idea to put it in production.

We will now move onto a more complex metric, the transaction rate, which is directly linked to the revenue. 

Let’s start with a scenario where the transaction rate goes up. You assume that you will get more transactions with the same traffic, so the only way it could be a bad thing is that you earn less in the end. This means your average cart value (AOV) has plummeted. The basic revenue formula shows it explicitly: 

Total revenue = traffic * transaction rate * AOV 

Since we consider traffic as an external factor, then the only way to have a higher total revenue is to have an increase in both transaction rate and AOV or have at least one of them increase while the other remains stable. This means we also need to check the AOV evolution, which is much more complicated. 

On the surface, it looks simple: take the sum of all transactions and divide that by the number of transactions and you have the AOV. While the formula seems basic, the data isn’t. In this case, it’s not just either success or failure; it’s different values that can widely vary.

Below is a histogram of transaction values from a retail ecommerce website. The horizontal axis represents values (in €), the vertical axis is the proportion of transactions with this value. Here we can see that most values are spread between 0 and €200, with a peak at ~€50. 


The right part of this curve shows a “long/fat tail”. Now let’s try to see how the difference within this kind of data is hard to spot. See the same graph below but with higher values, from €400 to €1000. You will also notice another histogram (in orange) of the same values but offset by €10.

We see that the €10 offset which corresponds to a 10-unit shift to the right is hard to distinguish. And since it corresponds to the highest values this part has a huge influence when averaging samples. Due to the shape of this transaction value distribution, any measure of the average value is somewhat blurred, which makes it very difficult to have clear statistical indices. For this reason, changes in AOV need to be very drastic or measured over a huge dataset to be statistically asserted,  making it difficult to use in CRO.

Another important feature is hidden even further on the right of the horizontal axis. Here’s another zoom on the same graph, with the horizontal axis ranging from €1000 to €4500. This time only one curve is shown.

From the previous graph, we could have easily assumed that €1000 was the end, but it’s not. Even with a most common transaction value at €50, there are still some transactions above €1000, and even some over €3000. We call these extreme values. 

As a result, whether these high values exist or not makes a big difference. Since these values exist but with some scarcity, they will not be evenly spread across a variation, which can artificially create difference when computing AOV. By artificially, we mean the difference comes from a small number of visitors and so doesn’t really count as “statistically significant”. Also, keep in mind that customer behavior will not be the same when buying for €50 as when making a purchase of more than €3000.

There’s not much to do about this except know it exists. One good thing though is to separate B2B and B2C visitors if you can, since B2C transaction values are statistically bigger and less frequent. Setting them apart will limit these problems.

What does this mean for AOV?

There are three important things  to keep in mind when it comes to AOV:

  1. Don’t trust the basic AOV calculation; the difference you are seeing probably does not exist, and is quite often not even in the same observed direction! It’s only displayed to give an order of magnitude to interpret changes in conversion rates but shouldn’t be used to state a difference between variations’ AOV. That’s why we use a specific test, the Mann-Whitney U test, that’s adapted for this kind of data.
  2. You should only believe the statistical index on AOV, which is only valid to assess the direction of the difference between AOV, not its size. For example, you notice a +€5 AOV difference and the statistical index is 95%; this only means that you can be 95% sure that you will have an AOV gain, but not that it will be €5.
  3. Since transaction data is far more wild than conversion data, it will need stronger differences or bigger datasets to reach statistical significance. But since there are always fewer transactions than visitors, reaching significance on the conversion rate doesn’t imply being significant on AOV.

This means that a decision on a variation that has a conversion rate gain can still be complex because we rarely have a clear answer about the variation effect on the AOV.

This is yet another reason to have a clear experimentation protocol including an explicit hypothesis. 

For example, if the test is about showing an alternate product page layout based on the hypothesis that visitors have trouble reading the product page, then the AOV should not be impacted. Afterwards, if the conversion rate rises, we can validate the winner if the AOV has no strong statistical downward trend. However, if the changes are in the product recommender system, which might have an impact on the AOV, then one should be more strict on measuring a statistical innocuity on the AOV before calling a winner. For example, the recommender might bias visitors toward cheaper products, boosting sales numbers but not the overall revenue.

The real driving force behind CRO

We’ve seen that the conversion rate is at the base of CRO practice because of its simplicity and versatility compared to all other KPIs. Nonetheless, this simplicity must not be taken for granted. It sometimes hides more complexity that needs to be understood in order to make profitable business decisions, which is why it’s a good idea to have expert resources during your CRO journey. 

That’s why at AB Tasty, our philosophy is not only about providing top-notch software but also Customer Success accompaniment.

Share on

LinkedIn Facebook Twitter

Article

Feb 2, 2024
10min read

A/A Testing: What is it and When Should You Use it?

Hubert Wassner

Hubert Wassner

A/A tests are a legacy from the early days of A/B testing. It’s basically creating an A/B test where two identical versions of a web page or element are tested against each other. Variation B is just a copy of A without any modification.

One of the goals of A/A tests is to check the effectiveness and accuracy of testing tools. The expectation is that, if no winner is declared, the test is a success. Whereas detecting a statistical difference would mean a failure, indicating a problem somewhere in the pipeline.

But it’s not always that simple. We’ll dive into this type of testing and the statistics and tech behind the scenes. We’ll look at why a failed A/A test is not a proof of pipeline failure, and that a successful A/A test isn’t a foolproof sanity check.

What is tested during an A/A test?

Why is there so much buzz around A/A testing? An A/A test can be a way to verify two components of an experimentation platform: 

  1. The statistical tool: It may be possible that the formulas chosen don’t fit the real nature of the data, or may contain bugs.
  2. The traffic allocation: The split between variations must be random and respect the proportions it has been given. When a problem occurs, we talk about Sample Ratio Mismatch (SRM); that is, the observed traffic does not match the allocation setting. This means that the split has some bias impacting the analysis quality.
    Let’s explore this in more detail.

Statistical tool test

Let’s talk about a “failed” A/A test

The most common idea behind A/A tests is that the statistical tool should yield no significant difference. It is considered a “failed” A/A test if you detect a difference in performance during an A/A test. 

However, to understand how weak this conclusion is, you need to understand how statistical tests work. Let’s say that your significance threshold is 95%. This means that there is still a 5% chance that the difference you see is a statistical fluke and no real difference exists between the variations. So even with a perfectly working statistical tool, you still have one chance in twenty (1/20=5%) that you will have a “failed” A/A test and you might start looking for a problem that may not exist.

With that in mind, an acceptable statistical procedure would be to perform 20 A/A tests and expect to have 19 that yield no statistical difference, and one that does detect a significant difference. And even in this case, if 2 tests show significant results, it’s a sign of a real problem. In other words, having 1 successful A/A test is in fact not enough to validate a statistical tool. To validate it fully, you need to show that the tests are successful 95% of the time (=19/20).

Therefore, a meaningful approach would be to perform hundreds of A/A tests and expect ~5% of them to “fail”. It’s worth noting that if it “fails” less than 5% of the time it’s also a problem, maybe indicating that the statistical test simply says “no” too often, leading to a strategy that never detects any winning variation. So one A/A “failed” test doesn’t tell much in reality. 

What if it’s a “successful A/A test”? 

A “successful” A/A test (yielding no difference) is not proof that everything is working as it should. To understand why, you need to check another important tool in an A/B test: the sample size calculator.

In the following example, we see that from a 5% conversion rate, you need around 30k visitors per variation to reach the 95% significance level if a variation yields a 10% MDE (Minimal Detectable Effect).

But in the context of an A/A test, the Minimal Detectable Effect (MDE) is in fact 0%. Using the same formula, we’ll plug 0% as MDE.

At this point, you will discover that the form does not let you put a 0% here, so let’s try a very small number then. In this case, you get almost 300M visitors, as seen below.

In fact, to be confident that there is exactly no difference between two variations, you need an infinite number of visitors, which is why the form does not let you set 0% as MDE.

Therefore, a successful A/A test only tells you that the difference between the two variations is smaller than a given number but not that the two variations perform exactly the same.

This problem comes from another principle in statistical tests: the power. 

The power of a test is the chance that you discover a difference if there is any. In the context of an A/A test, this refers to the chance you discover a statistically significant discrepancy between the two variations’ performance. 

The more power, the more chance you will discover a difference. To raise the power of a test you simply raise the number of visitors.

You may have noticed that in the previous screenshots, tests are usually powered at 80%. This means that even if a difference exists between the variations in performance, 20% of the time you will miss it. So one “successful” A/A test (yielding no statistical difference) may just be an occurrence of this 20%. In other words, having just one successful A/A test doesn’t ensure the efficiency of your experimentation tool. You may have a problem and there is a 20% chance that you missed it. Additionally, reaching 100% of power will need an infinite number of visitors, making it impractical.

How do we make sure we can trust the statistical tool then? If you are using a platform that is used by thousands of other customers, chances are that the problem would have already been discovered. 

Because statistical software does not change very often and it is not affected by the variation content (whereas the traffic allocation might change, as we will see later), the best option is to trust your provider, or you can double-check the results with an independent provider. You can find a lot of independent calculators on the web. They only need the number of visitors and the number of conversions for each variation to provide the results making it quick to implement.

Traffic allocation test

In this part, we only focus on traffic, not conversions. 

The question is: does the splitting operation work as it should? We call this kind of failure a SRM or Sample Ratio Mismatch. You may ask yourself how a simple random choice could fail. In fact, the failure happens either before or after the random choice. 

The following demonstrates two examples where that can happen:

  • The variation contains a bug that may crash some navigators. In this case, the corresponding variation will lose visitors. The bug might depend on the navigator and then you will end up with bias in your data.
  • If the variation gives a discount coupon (or any other advantage), and some users find a way to force their navigator to run the variation (to get the coupon), then you will have an excess of visitors for that variation that is not due to random chance, which results in biased data.


It’s hard to detect with the naked eye because the allocation is random, so you never get sharp numbers. 

For instance, a 50/50 allocation never precisely splits the traffic in groups with the exact same size. As a result, we would need statistical tools to check if the split observed corresponds with the desired allocation. 

SRM tests exist. They work more or less the same way as an A/B test except that the SRM formula indicates whether there is a difference between the desired allocation and what really happened. If there is indeed an SRM, then there is a chance that this difference is not due to pure randomness. This means that some data is lost or bias occurred during the experiment entailing trust for future (real) experiments.

On the one hand, detecting an SRM during an A/A test sounds like a good idea. On the other hand, if you think operationally it might not be that useful because the chance of a SRM is low.  

Even if some reports say that they are more frequent than you may think, most of the time it happens on complex tests. In that sense, checking SRM within an A/A test will not help you to prevent having one on a more complex experiment later. 

If you find a Sample Ration Mismatch on a real experiment or in an A/A test, the following actions remain the same: find the cause, fix it, and restart the experiment. So why waste time and traffic on an A/A test that will give you no information? A real experiment would have given you real information if it worked fine on the first try. If a problem does occur, we would detect it even in a real experiment since we only consider traffic and not conversions.

A/A tests are also unnecessary since most trustworthy A/B testing platforms (like AB Tasty) do SRM checks on an automated basis. So if an SRM occurs, you will be notified anyway. 

So where does this “habit” of practicing A/A tests come from?

Over the years, it’s something that engineers building A/B testing platforms have done. It makes sense in this case because they can run a lot of automated experiments, and even simulate users if they don’t have enough at hand, performing a sound statistical approach to A/A tests. 

They have reasons to doubt the platform in the works and they have the programming skills to automatically create hundreds of A/A tests to test it properly. Since these people can be seen as pioneers, their voice on the web is loud when they explain what an A/A test is and why it’s important (from an engineering perspective).

However, for a platform user/customer, the context is different as they’ve paid for a ready-to- use and trusted platform and can start a real experiment as soon as possible to get a return on investment. Therefore, it makes little sense to waste time and traffic on an A/A test that won’t provide any valuable information.

Why sometimes it might be better to skip A/A tests

We can conclude that a failed A/A test is not a problem and that a successful one is not  proof of sanity. 

In order to gain valuable insights from A/A tests, you would need to perform hundreds of them with an infinite number of visitors. Moreover, an efficient platform like AB Tasty does the corresponding checks for you.

That’s why, unless you are developing your own A/B testing platform, running an A/A test may not give you the insights you’re looking for. A/A tests require a considerable amount of time and traffic that could otherwise be used to conduct A/B tests that could give you valuable insights on how to optimize your user experience and increase conversions. 

When it makes sense to run an A/A test

It may seem that running A/A tests may not be the right call after all. However, there may be a couple of reasons why it might still be useful to perform A/A tests. 

First is when you want to check the data you are collecting and compare it to data already collected with other analytics tools but keep in mind that you will never get the exact same results. The reason is that most of the metric definitions vary on different tools. Nonetheless this comparison is an important onboarding step to ensure that the data is properly collected.

The other reason to perform an A/A test is to know the reference value for your main metrics so you can establish a baseline to analyze your future campaigns more accurately. For example, what is your base conversion rate and/or bounce rate? Which of these metrics need to be improved and are, therefore, a good candidate for your first real A/B test?

This is why AB Tasty has a feature that helps users build A/A tests dedicated to reach these goals and avoids the pitfalls of “old school”  methods that are not useful anymore. With our new A/A test feature, A/A test data is collected in one variant (not two); let’s call this an “A test”. 

This allows you to have a more accurate estimation of these important metrics as the more data you have, the more accurate the measurements are. Meanwhile, in a classic A/A test, data is collected in two different variants which provides less accurate estimates since you have less data for each variant.

With this approach, AB Tasty enables users to automatically set up A/A tests, which gives better insights than classic “handmade” A/A tests.

Share on

LinkedIn Facebook Twitter